J(y( . )) = 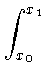 y(x) y(x)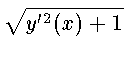 dx , dx ,
|
(1) |
Задача о минимальной поверхности вращения сводится (см., например [1, 2, 4, 6]), к нахождению минимума функционала
при условии
y(x)![]() 0 и граничных условиях
0 и граничных условиях
Легко показать (см. [1, 2, 3, 4, 5, 6]), что общим решением уравнения Эйлера в этой задаче будет цепная линия
где a, b - константы, которые необходимо подобрать так, чтобы удовлетворить граничным условиям (2).
Полное рассмотрение зависимости a и b от (x0, y0) и требует сложных и громоздких выкладок. Поэтому здесь мы рассмотрим упрощенный вариант граничных условий, для которого, тем не менее, хорошо видны проблемы, возникающие при поиске a и b.
Итак, пусть
Из уравнений (4) и (3) следует h = 0. Таким образом задача нахождения коэффициентов в нашем случае сводится к нахождению только коэффициента a, такого, чтобы выполнялось
|
h = acosh |
(5) |
Это уравнение трансцендентно относительно a и не разрешается аналитически. Для точного нахождения a для конкретного значения h необходимо применять численные методы1.
Рассмотрим как задачу поиска a можно решить геометрически.
Запишем (5) по-другому:
Введем переменную y* и запишем (6) в виде системы:
Сделаем замену x* = 1/a и перепишем (7) в
виде
Таким образом мы свели задачу поиска a к задаче поиска точки (точек) пересечения прямой y = hx и гиперболической косинусоиды y = cosh x; если нам известна абсцисса x* точки пересечения этих кривых, то коэффициент a, соответствующий h будет равен
(По сути дела мы получаем искомую кривую
y = acosh![]() из
кривой y = cosh x путем применения к ней гомотетии с
коэффициентом
из
кривой y = cosh x путем применения к ней гомотетии с
коэффициентом
![]() с центром в точке O(0, 0).
с центром в точке O(0, 0).
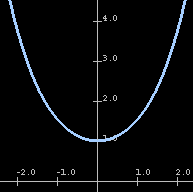 Рис. 1 |
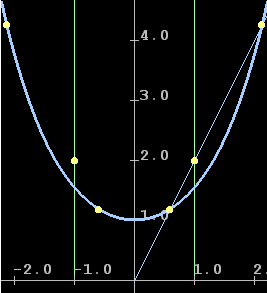 Рис. 2 |
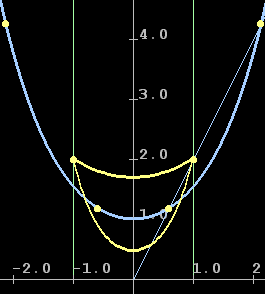 Рис. 3 |
Из рисунков видно, что при уменьшении h наступает случай, когда у системы (8) нет ни одного решения. Аналогичный факт показан в литературе ([1, 2, 3, 4, 7]) и для общего случая граничных условий: существует область допустимых (в смысле постановки задачи) граничных условий для которых не существует решение уравнения Эйлера (нельзя подобрать коэффициенты a и b, чтобы удовлетворить (2)).
Ниже (рис. 4) приведена программа (апплет) которая решает задачу решения системы (8) "геометрически2". Страница с большим вариантом апплета расположена здесь. (Внимание: для верной работы страницы с большим вариантом Ваша программа просмотра должна поддерживать JavaScript, запасной вариант без JavaScript здесь.)
Рис. 4 |
Программа предназначена, в основном, для демонстрации слушателям при рассмотрении предмета, то есть как инструмент лектора, но, возможно, будет интересна и индивидуально обучающимся. Желающие использовать апплет отсылаются к техническому описанию апплета, там же есть и двоичный код.
Исходно апплет изображает график функции y = cosh x. Желаемую величину h можно ввести нажав левую кнопку мыши -- вертикальная координата "клика" соответствует h. Для запуска анимации процесса гомотетии нажмите клавишу на клавиатуре или правую клавишу мыши. Для прекращения процесса анимации нажмите клавишу на клавиатуре или выберите новое значание h нажатием левой клавиши мыши.
Автор благодарит Моргунову Наталью Николаевну за незаменимую помощь при переводе статьи из LATEX'а в HTML.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_math -html_version 3.2,math -prefix pmrsd pmrs.tex.
The translation was initiated by Ivanov on 1999-02-11
Кроме того, естественно, много подправлено "ручками". (А.Иванов)
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru