Необходимо отыскать образующую поверхности вращения, которая минимизировала бы площадь этой поверхности. Известно, что искомая образующая -- цепная линия (гиперболический косинус). В зависимости от конкретных граничных условий могут существовать два решения уравнения Эйлера (каждое -- цепная линия), одно или ни одного.
При традиционном изложении, как правило, останавливаются на задаче
выбора оптимальной из двух кривых и не уделяют внимания случаю
отсутствия классического решения. При численном решении методом Эйлера
легко обнаруживается разрывное решение: два диска, образующей для которых
служит ломаная, состоящая из двух вертикальных отрезков и одного
горизонтального, лежащего на оси Ox.
В [1] доказывается, что разрывное решение всегда является локальным минимумом.
Более того, даже в области существования решения уравнения Эйлера можно
численно найти подобласть, где глобальный минимум достигается на разрывном
решении.
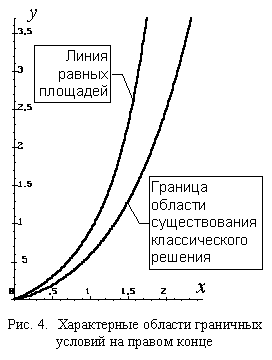
На рис. 4 эта подобласть расположена между
"Линией равных площадей" и "Границей области существования классического
решения" (граничные условия на левом конце фиксированы: x0=0, y0=1).
Ведутся работы
|
Для построения оптимального решения "кликните" мышкой в первом квадранте черного поля. В режиме "STEREO" работают клавиши: 1, 2, 3, 4, 5, 6, 7, 8, 9, G, C, стрелка_вверх, стрелка_влево, стрелка_вправо, стрелка_вниз. |
Ведутся работы
Вариационное исчисление | Главное меню | Новости | Публикации |
iagsoft@imm.uran.ru