От составителя
Это издание является перепечаткой страниц 376-388 из книги

И.Ньютон. Математические начала натуральной философии.
Перевод с латинского А.Н.Крылова. Книги II и III. Петроград,
тип. М.М.Стасюлевича, 1916.
Работа выполнена в рамках проекта “Классические задачи вариационного
исчисления”,
раздел “Аэродинамическая задача Ньютона”.
При переводе в электронный вид буква “и с точкой” (i) заменена
на “и”, буква “ять” заменена на “е”, убраны твердые знаки
в конце слов. Нижняя точка “.” как знак умножения заменена на
центральную точку “ . ”.
В остальном сохранена оригинальная орфография,
исправлены только явные опечатки.
Номера подстрочных примечаний
(примечания и пояснения А.Н.Крылова) и номера рисунков
совпадают с номерами в оригинале. Замечания на полях
(в печатной версии) добавлены мной
(А.И.).
Я буду благодарен всем, кто сообщит о замеченных опечатках
и неточностях (адрес электронной почты: iagsoft@imm.uran.ru).
Составитель выражает благодарность Г.Ф.Корниловой и
Н.Н.Моргуновой
за помощь в “борьбе” с LATEX 'ом. А также
Институту математики и механики УрО РАН, на чьей технике производились работы.
P.S. (25.01.2007): Обнаружена полная электронная копия издания "Начал..." в переводе
А.Н.Крылова в формате Djvu:
здесь
и
здесь.
О Т Д Е Л VII.
О движении жидкостей и сопротивлении брошенных
тел.
Предложение XXXII. Теорема XXVI.
Пусть две материальныя системы подобны между собою и состоят из одинаковаго
числа подобным образом расположенных частиц, причем каждая частица одной
системы подобна, и масса ея пропорциональна массе частицы ей
соответствующей другой системы, и плотности частиц находятся в постоянном
отношении; пусть эти частицы по npoшecmвии пропорционалъных промежутков
времени начинают двигаться подобным образом (принадлежащия одной системе
друг по отношению к другу и принадлежащия другой также друг относительно
друга); если при этом частицы той же системы не касаются друг друга, за
исключением моментов соударений, взаимно не притягиваются и не
отталкиваются ни с какими силами, за исключением ускорительных сил обратно
пропорциональных линейным размерениям соответствующих частиц и прямо
пропорциональных квадратам их скоростей, то я утверждаю, что частицы каждой
из этих систем будут продолжать находиться в конце пропорциональных
промежутков времени в подобном друг относительно друга движении.
Я называю движения подобных и, по прошествии пропорциональных промежутков
времени, подобным образом расположенных тел подобными, когда в конце любых
таковых промежутков времени относительное расположение этих тел подобно,
предполагая, что частицы одной системы сопоставляются с соответствующими
частицами другой. Поэтому промежутки времени, в продолжение которых
соответствующия частицы описывают подобныя и пропорциональныя части подобных
фигур пропорциональны. Следовательно, если имеются две системы такого рода,
то соответствующия частицы вследствие подобия начальных движений будут
продолжать двигаться подобным образом, пока не встретятся, ибо, если
на эти частицы никакия силы не действуют, и по Закону I оне будут двигаться
равномерно и прямолинейно; если же оне действуют друг на друга с какими-либо
ускорительными силами, обратно пропорциональными линейным размерениям
соответствующих частиц и прямо пропорциональными квадратам скоростей, то, в
виду подобия расположения частиц и пропорциональности этих сил, полныя
ускорительныя силы действующия на частицы, слагающияся, по 2ому следствию
законов, из частных будут направлены сходственным образом, т.-е. как будто
бы к сходственно между частицами расположенным центрам; эти полныя силы
будут относиться между собою как и их составляющия, т.-е. будут обратно
пропорциональны линейным размерам соответствующих частиц и прямо
пропорциональны квадратам их скоростей, поэтому вследствие действия таких
сил соответствующия частицы будут продолжать описывать подобныя фигуры. Это
будет происходить таким образом (по сл. 1 и 8, IV предл. 1-ой книги), когда
эти кажущиеся центры будут находиться в покое. Но и тогда, когда эти центры
будут двигаться, расположение их относительно частиц в виду подобия
перемещений, остается сходственным, значит и производимыя изменения в
фигурах описываемых частицами будут подобны.
Следовательно, движения соответствующих и сходственных частиц будут
оставаться подобными до первой их встречи друг с другом, а так как эта
встреча и удар будут подобны, то будет подобно и отражение и значит (по выше
показанному) вновь будет подобное относительное движение частиц, пока снова
не произойдет удар, и так будет продолжаться до безконечности.
Следствие 1. Таким образом, если два каких-либо подобных между собою тела,
расположенных сходственнымъ образом по отношению к соответствующим частицам,
начнут по прошествии пропорциональных промежутков времени двигаться подобным
образом и если их величины и плотности находятся в том же отношении, как
величины и плотности соответствующих частиц, то в конце пропорциональных
промежутков времени эти тела будут продолжать двигаться подобным образом.
Ибо все, относящееся до частиц обеих систем в равной мере относится и до
больших частей их.
Следствие 2. Если все подобныя и подобным образом расположенныя части
систем находятся в относительном пoкoe, и две из этих частей, которыя больше
прочих, и в обеих системах соответствуют друг другу, начнут двигаться
подобным образом по линиям сходственным образом расположенным, то оне
произведут в прочих частях системы подобныя движения и в конце
пропорциональных промежутков времени будут продолжать двигаться между ними
подобным образом, описывая при этом пространства пропорциональныя своим
линейным размерениям.
Предложение XXXIII. Теорема XXVII.
При тех же предположениях я утверждаю, что большия части систем будут
испытыват сопротивления пропорциональныя: квадратам их скоростей,
квадратам линейных размерений и плотностям частей систем.
Сопротивление происходит частию от центробежных и центростремительных сил
взаимодействия между частицами, частию от ударов частиц о большия части
систем и отражений от них.
Сопротивления перваго рода относятся между собою, как полныя движущия силы,
от коих они происходят, т.-е. как произведения полных ускорительных сил на
массы соответствующих частей; по предположению это одинаково с прямою
пропорциональностью квадратам скоростей и массам соответствующих частей и
обратною пропорциональностью разстояниям между соответствующими частицами;
но разстояния между частицами одной системы относятся к разстояниям между
частицами другой как диаметры этих частиц или как размеры частей одной
системы к размерам соответствующих частей другой, массы же пропорциональны
плотностям этих частей и кубам ихъ размеров, следовательно, сопротивления
будут пропорциональны квадратам скоростей, квадратам сходственных размерений
и плотностям частей систем.
Сопротивления второго рода пропорциональны числу и силе соответствующих
ударов и отражений. Числа отражений прямо пропорциональны скоростям
соответствующих частиц и обратно пропорциональны разстояниям между местами
их встреч. Силы же отражений пропорциональны скоростям, объемам и плотностям
соответствующих частей, т.-е. скоростям, кубам размерений и плотностям
частей. По перемножении всех этих отношений окажется, что сопротивления,
испытываемыя соответствующими частями систем, относятся между собою как
произведения квадратов скоростей на квадраты линейных размерений и на
плотности частей.
Следствие 1. Поэтому, если обе эти системы представляют две упругих жидкости
в родe воздуха, и частицы их находятся в относительном покое для каждой
системы, два же подобных тела, по величине и плотности пропорциональных
частицам жидкости и расположенных сходственным образом между этими
частицами ея, будут брошены как бы то ни было по линиям, также сходственно
расположенным, то, так как ускорительныя силы взаимодействий между частицами
обратно пропорциональны диаметрам брошенных тел и прямо пропорциональны
квадратам их скоростей, тела эти в пропорциональные промежутки времени будут
возбуждать подобныя движения в жидкости и будут описывать подобныя
пространства, относящиеся между собою как линейныя размерения этих тел.
Следствие 2. Отсюда следует, что быстро движущееся тело испытывает в той же
самой жидкости сопротивление, приблизительно пропорциональное квадрату
скорости. Ибо, если бы силы, с которыми находящияся на разстоянии частицы
действуют друг на друга, увеличивались бы как квадраты скоростей, то
сопротивление было бы также в точности пропорционально квадрату скорости;
таким образом в средe, частицы которой находящияся в некотором разстоянии друг
от друга совсем не оказывают взаимодействий, сопротивление в точности
пропорционально квадрату скорости. Пусть имеется три среды A, B, C,
состоящия из равных и подобных частиц правильно расположенных на равных друг
от друга разстояниях. Частицы сред A и B взаимно отталкиваются с силами,
относящимися между собою как T к V, частицы же среды C таковыми силами
совершенно не обладают. Если в этих средах будут двигаться четыре равных
тела D, E, F, G — первыя два соответственно в средах A и B
последния два в
среде C, причем отношение скорости тела D к скорости тела E и отношение
скорости тела F к скорости тела G равно
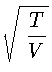 , тогда сопротивление
тела D будет
относиться к сопротивлению тела E, и сопротивление тела F к сопротивлению
тела G, как квадраты их скоростей, поэтому и отношение сопротивления тела D
к сопротивлению тела F будет равно отношению сопротивления тела E к
сопротивлению тела G. Положим теперь, что скорости тел D и F равны, так же и
скорости тел E и G; увеличивая скорости тел D и F в любом отношении и
уменьшая силы взаимодействия частиц среды B в таком же отношении, но
возвышенном в квадрат, можно приблизить сколь угодно среду B к виду и
ycлoвиям среды C, значит и сопротивления равных и обладающих равными
скоростями тел E и G, в этих средах будут приближаться к равенству так, что
разность между этими сопротивлениями может быть сделана меньше любой заданной
величины. Так как сопротивления D и F относятся между собою как
сопротивления тел E и G, то и они приблизятся также к равенству. Таким
образом, когда тела D и F движутся весьма быстро, то сопротивления их весьма
близки к равенству, и так как сопротивление тела F пропорционально квадрату
скорости, то и сопротивление тела D будет приблизительно следовать тому же
закону.
, тогда сопротивление
тела D будет
относиться к сопротивлению тела E, и сопротивление тела F к сопротивлению
тела G, как квадраты их скоростей, поэтому и отношение сопротивления тела D
к сопротивлению тела F будет равно отношению сопротивления тела E к
сопротивлению тела G. Положим теперь, что скорости тел D и F равны, так же и
скорости тел E и G; увеличивая скорости тел D и F в любом отношении и
уменьшая силы взаимодействия частиц среды B в таком же отношении, но
возвышенном в квадрат, можно приблизить сколь угодно среду B к виду и
ycлoвиям среды C, значит и сопротивления равных и обладающих равными
скоростями тел E и G, в этих средах будут приближаться к равенству так, что
разность между этими сопротивлениями может быть сделана меньше любой заданной
величины. Так как сопротивления D и F относятся между собою как
сопротивления тел E и G, то и они приблизятся также к равенству. Таким
образом, когда тела D и F движутся весьма быстро, то сопротивления их весьма
близки к равенству, и так как сопротивление тела F пропорционально квадрату
скорости, то и сопротивление тела D будет приблизительно следовать тому же
закону.
Следствие. 3. Сопротивление тела движущагося весьма быстро во всякой
упругой жидкости почти такое же, как если бы частицы жидкости были лишены
отталкивательных сил; в упругих жидкостях сила упругости происходит от
отталкивательных сил частиц и надо, чтобы скорость была настолько велика,
чтобы эти силы не имели достаточно времени, чтобы проявить свое действие.
Следствие 4. Так как сопротивление тел подобных и обладающих одинаковыми
скоростями в среде, частицы которой взаимно не отталкиваются
пропорционально квадратам линейных размерений, то и сопротивления
тел движущихся с равными весьма большими скоростями в упругой
жидкости будут приблизительно пропорциональны квадратам этих размерений.
Следствие 5. В срединах той же самой плотности, частицы которых взаимно не
отталкиваются, но могут быть как большими и в небольшом числе, так и малыми
и многочисленными, тела подобныя, равныя и движущияся с одинаковыми
скоростями в равныя времена встречают одинаковое количество материи и
сообщают ему тоже самое количество движения и следовательно (по
3-му Закону) испытывают и равное противодействие, т.-е. претерпевают одинаковое
сопротивление; поэтому очевидно, что при весьма быстром движении в упругих
жидкостях той же самой плотности сопротивления приблизительно равны
независимо от того, состоят ли эти жидкости из более грубых частиц или же из
самых мельчайших. От большей тонкости жидкости сопротивления снарядов
движущихся весьма быстро не уменьшилось бы значительно.
Следствие 6. Все изложенное выше имеет место в таких упругих жидкостях,
коих сила упругости происходит от отталкивательных сил между частицами.
Если же эта сила происходит от чего-либо иного, как напр., от расположения
частиц на подобие шерсти или ветвей дерева, или от всякой иной причины, по
которой относительныя движения становятся менее свободными, то сопротивление
вследствие меньшей текучести жидкости станет больше, нежели в предыдущих
случаях.
Предложение XXXIV. Теорема XXVIII.
Если шар и цилиндр, описанные на равных диаметрах, движутся с одинаковой
скоростью по направлению оси цилиндра, в редкой среде состоящей из равных
частиц свободно расположенных в равных друг от друга разстояниях, то
сопротивление шара вдвое меньше сопротивления цилиндра.
Так как действие среды на тело то же самое (по след. 5 законов), движется
ли тело в покоющейся среде, или же частицы среды ударяют с тою же скоростью
на покоющееся тело, то будем разсматривать, что тело в покое и посмотрим
какой напор будет на него действовать от движущейся среды. Пусть ABKJ
(фиг. 168)
представляет шар, описанный из центра C радиусом CA,
и частицы среды
ударяют его с постоянною скоростью по прямым линиям, направленным
параллельно прямой AC, пусть FB есть одна из этих прямых линий. Отложим по
FB длину LB равную радиусу CB и проведем касательную BD к шару в точке B;
на KC и BD опустим перпендикуляры BE и LD, сила, с которою частица среды,
падая наклонно по прямой FB, ударяет шар в точке B, относится к той силе, с
которою та же частица ударила бы цилиндр в точке b, как LD к LB или как
BE к BC.
Затем на движение шара по направлению линии падения FB или AC действительною
оказывается от полной силы удара направленной по BC лишь слагающая по
направлению FB, относящаяся к этой полной силе как BE к BC. Из перемножения
этих отношений следует, что действующая по направлению FB слагающая силы
удара частицы на шар, относится к действующей по этому же направлению
слагающей силы удара частицы на цилиндр, как BE2 относится к BC2.
Поэтому,
если по перпендикуляру bE к основанию NAO цилиндра отложить длину bH так,
чтобы было
bH : BE = BE : CB, то отношение bH к bE будет равно отношению
вышеупомянутых действий силы удара на шар и на цилиндр, следовательно объем,
занятый всеми прямыми bH, находится к объему, занятому прямыми bE в том же
отношении, как действие всех частиц на шар к действию их на
цилиндр 161)
Но первый объем есть параболоид, коего вершины C, ось CA и параметр CA,
второй же объем есть цилиндр около этого параболоида
описанный, известно, что объем параболоида равен половине объема описаннаго
цилиндра. Следовательно, полная сила действия среды на шар равна половине
таковой же силы на цилиндр, поэтому, если бы частицы среды находились в
покое, цилиндр же и шар двигались с одинаковою скоростью, сопротивление
шара было бы вдвое меньше сопротивления цилиндра.
Поучение.
По этому способу можно сравнивать сопротивления и других фигур между собою,
а также находить те, которыя наиболее приспособлены к продолжению своего
движения в сопротивляющейся среде. Так, если на круговом основании CEBH
(фиг. 169), описанном из центра O радиусом OC требуется построить такой
усеченный конус CBFG с высотою OD, коего сопротивление было бы меньше
сопротивления всякаго другого усеченнаго конуса, построеннаго на том же
основании и высоте и движущагося по оси OD в сторону D, то,
разделив высоту
OD в точке Q пополам, продолжи OQ до S так, чтобы было
QS = QC
S и будет вершиною искомаго конуса, который усекается 162).
Здесь же заметим мимоходом, что угол CSB (фиг. 170) всегда острый, поэтому,
если тело ADBE образуется обращением эллипса или овала
ADBE около оси AB и к производящей кривой проводятся касательныя
FG, GH, HI
в точках F, B и I так, что GH перпендикулярно к оси
AB в точке касания B,
другия же две касательныя FG и HI coставляют с GH углы
FGB и IHB равные
135°, то тело, образуемое обращением фигуры ADFGHIE около той же оси
AB
будет испытывать меньшее сопротивление, нежели первоначальное при движении
вдоль своей оси точкою B вперед. Я считаю, что это предложение может быть не
безполезно при построении судов 163).
Когда же фигура DNFG будет кривою такого рода, что если из любой ея точки
N
опустить на ось перпендикуляр NM и из заданной точки G провести
прямую GR
параллельную касательной к кривой в точке N и пересекающую ось в точке
R, то имеет место пропорция:
MN : GR = GR3 : BR . GB2
тогда тело, образующееся при обращении этой кривой около оси AB
при движении
в вышеупомянутой редкой среде в направлении от A к B будет испытывать
меньшее сопротивление, нежели всякое иное тело вращения, описанное на той
же длине и той же наибольшей ширине 164).
Предложение XXXV. Задача VII.
Предполагая, что редкая среда состоит из равных, весьма малых, покоющихся
частиц, свободно расположенных в равных друг от друга разстояниях, требуется
определить сопротивление, испытываемое равномерно движущимся в такой среде
шаром.
Случай 1. Вообразим, что цилиндр, диаметр и высота коего равны
диаметру шара, движется с такою же скоростью, как и шар по направлению своей
оси в той же среде. Положим, что частицы среды, на которыя наталкивается
цилиндр или шар, отражаются с наибольшею силою. По предыдущему предложению
сопротивление шара вдвое меньше сопротивления цилиндра, объем шара
составляет
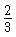 объема цилиндра, и цилиндр ударяя частицы нормально и
отражая их с наибольшею силою, сообщает им скорость вдвое большую своей
собственной, поэтому в продолжение того времени, как он равномерно проходит
путь, равный половине длины своей оси, он сообщит частицам количество
движения, так относящееся к количеству движения его самого, как плотность
жидкости относится к плотности этого цилиндра. Шар сообщит частицам такое же
количество движения в продолжение того времени, в которое он равномерно
проходит путь, равный своему диаметру; в то же время, как он проходит
объема цилиндра, и цилиндр ударяя частицы нормально и
отражая их с наибольшею силою, сообщает им скорость вдвое большую своей
собственной, поэтому в продолжение того времени, как он равномерно проходит
путь, равный половине длины своей оси, он сообщит частицам количество
движения, так относящееся к количеству движения его самого, как плотность
жидкости относится к плотности этого цилиндра. Шар сообщит частицам такое же
количество движения в продолжение того времени, в которое он равномерно
проходит путь, равный своему диаметру; в то же время, как он проходит
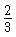 своего диаметра, сообщит частицам количество движения, относящееся к
полному количеству движения его самого как плотность среды к плотности шара.
Поэтому шар испытывает сопротивление так относящееся к силе, которая могла бы
поглотить или образовать полное его количество движения, в продолжение того
времени, как шар проходит равномерно путь, равный двум третям своего
диаметра, как плотность среды относится к плотности шара.
своего диаметра, сообщит частицам количество движения, относящееся к
полному количеству движения его самого как плотность среды к плотности шара.
Поэтому шар испытывает сопротивление так относящееся к силе, которая могла бы
поглотить или образовать полное его количество движения, в продолжение того
времени, как шар проходит равномерно путь, равный двум третям своего
диаметра, как плотность среды относится к плотности шара.
Случай 2. Положим, что частицы среды, встречаемыя шаром или цилиндром не
отражаются, тогда цилиндр при нормальном ударе будет сообщать этим частицам
скорость лишь равную своей собственной, и будет испытывать сопротивление,
равное половине предыдущаго, сопротивление шара составит также половину
предыдущаго.
Случай 3. Предположим теперь, что частицы среды обладают некоторою
силою отражения, которая меньше наибольшей и не равна нулю, но средняя между
этою наибольшею и нулевой, тогда и сопротивление шара будет средним и
находящимся в таком же отношении к сопротивлению в первом и во втором случае.
Следствие 1. Таким образом, если шар и частицы безконечно тверды и лишены
всякой упругости, а значит, и всякой силы отражения, то сопротивление шара
относится к силе, которая может поглотить или образовать полное его
количество движения в продолжение того времени, в которое шар проходит путь
равный четырем третям своего диаметра, как плотность среды относится к
плотности шара.
Следствие 2. Сопротивление шара при прочих одинаковых условиях
пропорционально квадрату скорости.
Следствие 3. Сопротивление шара при прочих одинаковых условиях
пропорционально квадрату диаметра.
Следствие 4. Сопротивление шара при прочих одинаковых условиях
пропорционально плотности среды.
Следствие 5. Сопротивление шара пропорционально квадрату скорости, квадрату
диаметра и плотности среды.
Следствие 6. Движение шара при таком сопротивлении может быть представлено
так: пусть AB (фиг. 171) представляет то время, в продолжение котораго шар
может утратить все свое количество движения, если принять сопротивление
постоянным и равным начальному; к AB проводим перпендикуляры AD и
BC и по BC
откладываем длину BC, изображающую полное начальное количество движения
шара; через точку C проводится гипербола CF, имеющая своими ассимптотами
прямыя AD и AB. Продолжим AB до какой-либо точки E и возставим перпендикуляр
EF, пересекающий гиперболу в точке F. Дополнив параллелограмм BCGE, проводим
прямую AF, пересекающую BC в H. Если шар в течение какого-либо времени BE,
продолжая двигаться равномерно в среде не сопротивляющейся, описал бы
пространство, представляемое площадью CBEG паралелограмма, то в
сопротивляющейся среде он опишет пространство представляемое гиперболическою
площадью CBEF, и количество его движения в конце сказаннаго времени
представится ординатою гиперболы EF, за утратою части FG. Сопротивление шара
в конце того же времени представится длиною BH, за утратою части HC
начальнаго сопротивления. Все это следует из предл. V, 2-ой книги, сл. 1 и 3.
Следствие 7. Таким образом, если шар в течение времени T, предполагая, что
сопротивление R остается постоянным, утрачивает полное свое количество
движения M, то этот шар в продолжение времени t утратит вследствие
сопротивления среды, уменьшающегося вместе со
скоростью пропорционально квадрату ея, количество движения равное
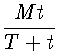 и остающаяся его часть составит
и остающаяся его часть составит
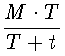 при этом шар пройдет путь,
длина коего относится к пути, описываемому во время t равномерно с такою
скоростью, при которой количество движения равно M, как
2,302585092994 . log
при этом шар пройдет путь,
длина коего относится к пути, описываемому во время t равномерно с такою
скоростью, при которой количество движения равно M, как
2,302585092994 . log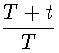 :
: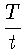 ибо отношение
площади BCFF гиперболы к площади BCGE равно такой величине.
ибо отношение
площади BCFF гиперболы к площади BCGE равно такой величине.
© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000
Версию этих страниц для печати можно скачать здесь.
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru

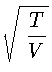 , тогда сопротивление
тела D будет
относиться к сопротивлению тела E, и сопротивление тела F к сопротивлению
тела G, как квадраты их скоростей, поэтому и отношение сопротивления тела D
к сопротивлению тела F будет равно отношению сопротивления тела E к
сопротивлению тела G. Положим теперь, что скорости тел D и F равны, так же и
скорости тел E и G; увеличивая скорости тел D и F в любом отношении и
уменьшая силы взаимодействия частиц среды B в таком же отношении, но
возвышенном в квадрат, можно приблизить сколь угодно среду B к виду и
ycлoвиям среды C, значит и сопротивления равных и обладающих равными
скоростями тел E и G, в этих средах будут приближаться к равенству так, что
разность между этими сопротивлениями может быть сделана меньше любой заданной
величины. Так как сопротивления D и F относятся между собою как
сопротивления тел E и G, то и они приблизятся также к равенству. Таким
образом, когда тела D и F движутся весьма быстро, то сопротивления их весьма
близки к равенству, и так как сопротивление тела F пропорционально квадрату
скорости, то и сопротивление тела D будет приблизительно следовать тому же
закону.
, тогда сопротивление
тела D будет
относиться к сопротивлению тела E, и сопротивление тела F к сопротивлению
тела G, как квадраты их скоростей, поэтому и отношение сопротивления тела D
к сопротивлению тела F будет равно отношению сопротивления тела E к
сопротивлению тела G. Положим теперь, что скорости тел D и F равны, так же и
скорости тел E и G; увеличивая скорости тел D и F в любом отношении и
уменьшая силы взаимодействия частиц среды B в таком же отношении, но
возвышенном в квадрат, можно приблизить сколь угодно среду B к виду и
ycлoвиям среды C, значит и сопротивления равных и обладающих равными
скоростями тел E и G, в этих средах будут приближаться к равенству так, что
разность между этими сопротивлениями может быть сделана меньше любой заданной
величины. Так как сопротивления D и F относятся между собою как
сопротивления тел E и G, то и они приблизятся также к равенству. Таким
образом, когда тела D и F движутся весьма быстро, то сопротивления их весьма
близки к равенству, и так как сопротивление тела F пропорционально квадрату
скорости, то и сопротивление тела D будет приблизительно следовать тому же
закону.
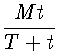 и остающаяся его часть составит
и остающаяся его часть составит
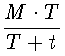 при этом шар пройдет путь,
длина коего относится к пути, описываемому во время t равномерно с такою
скоростью, при которой количество движения равно M, как
2,302585092994 . log
при этом шар пройдет путь,
длина коего относится к пути, описываемому во время t равномерно с такою
скоростью, при которой количество движения равно M, как
2,302585092994 . log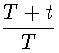 :
: iagsoft@imm.uran.ru
iagsoft@imm.uran.ru