Математические начала натуральной философии.
Отдел VII
"О движении жидкостей и сопротивлении брошенных тел"

Примечания и комментарии А.Н.Крылова

© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... на цилиндр 161)

      В этом предложении, как видно, попутно устанавливается закон пропорциональности сопротивления испытываемаго элементом поверхности квадрату синуса угла встречи.

      Ньютон разсматривает здесь жидкость как бы состоящей из отдельных независимых частиц движущихся на встречу телу с одною и тою же скоростью как по величине, так и по направлению. Обозначим эту скорость через V, она представлена на чертеже длиною BF. Нормаль к элементу поверхности шара в точке B направлена к радиусу BC, угол FBD = $ \alpha$, между направлением скорости и ея проекции на касательную плоскость, называется углом встречи.

      Под словом «сила удара», «сила действия частицы по направлению BE» и т. п. надо разуметь количество движения сообщаемое частицею ударяемому телу и его проекцию на указанное направление; эти количества движения пропорциональны полному количеству движения частицы и его проекции на соответствующее направление.

      Таким образом проекция количества движения частицы, масса которой m, на направление нормали BC будетъ mVsin$ \alpha$, и количество движения, сообщенное телу ударом, будет направлено по BC и пропорционально mVsin$ \alpha$ так, что его можно обозначить через kmVsin$ \alpha$, где k некоторая постоянная, проекция этого количества движения на направление CA будет kmVsin2$ \alpha$, но sin2$ \alpha$ = BE2 : CB2. Этой же проекции количества движения пропорциональна и составляющая силы сопротивления испытываемаго телом по направлению AC, происходящая от разсматриваемаго элемента поверхности подвергнувшагося удару.

      Вычисление отношения сопротивления шара к сопротивлению описаннаго около него цилиндра, коего производящия параллельны направлению движения, заключает еще неявно предположение, что число ударяющих частиц пропорционально величине элемента поверхности или его проекции на плоскость перпендикулярную к направлению движения, ибо лишь при этом предположении сопротивления шара и цилиндра представляются указанными объемами параболоида и цилиндра с таким же основанием и высотою; это предположение и оговорено в условии теоремы, — что частицы распределены равномерно.

© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... который усекается 162)

      Обозначим OD через 2a, OC через r, OS через x и через k постоянный множитель. Сопротивление испытываемое усеченным конусом при движении по направлению своей оси слагается из сопротивления на малое основание, пропорциональное площади этого основания, и проекции на ось сопротивления действующаго на боковую поверхность; на каждый элемент этой поверхности действует нормальное сопротивление пропорциональное величине этого элемента и квадрату синуса угла встречи равнаго CSO, таким образом сумма проекций всех этих элементарных сопротивлений на ось получится если умножить на sin2CSO сопротивление, которое действовало бы на кольцевую площадь равную разности площадей большого и малаго оснований конуса.

      Таким образом полное сопротивление R будет:

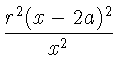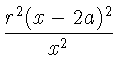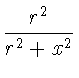
R = k$\displaystyle \left[\vphantom{ \displaystyle\frac {r^2(x-2a)^2}{x^2} + \left( r... ...frac {r^2(x-2a)^2}{x^2} \cdot \displaystyle\frac {r^2}{r^2+x^2} \right)}\right.$$\displaystyle {\frac{r^2(x-2a)^2}{x^2}}$ + $\displaystyle \left(\vphantom{ r^2 - \displaystyle\frac {r^2(x-2a)^2}{x^2} \cdot \displaystyle\frac {r^2}{r^2+x^2} }\right.$r2 - $\displaystyle {\frac{r^2(x-2a)^2}{x^2}}$ . $\displaystyle {\frac{r^2}{r^2+x^2}}$ $\displaystyle \left.\vphantom{ r^2 - \displaystyle\frac {r^2(x-2a)^2}{x^2} \cdot \displaystyle\frac {r^2}{r^2+x^2} }\right)$ $\displaystyle \left.\vphantom{ \displaystyle\frac {r^2(x-2a)^2}{x^2} + \left( r... ...frac {r^2(x-2a)^2}{x^2} \cdot \displaystyle\frac {r^2}{r^2+x^2} \right)}\right]$ = kr2 . 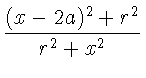$\displaystyle {\frac{(x-2a)^2 + r^2}{r^2+x^2}}$.

      Величина x обращающая сопротивление R в minimum определяется уравнением:

x2 - 2ax - r2 = 0,
положительный корень котораго
x = a + $\displaystyle \sqrt{a^2+r^2}$
отвечающий вопросу и строится описанным в тексте способом.

© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... построении судов 163)

      Доказательство этого свойства требует уже соображений составляющих как бы переходную ступень к тем, которыя теперь относятся к вариационному исчислению. Прежде всего заместим (черт. 170а), что когда высота a отсека конуса приближается к нулю, то x приближается к r и угол составляемый производящей с осью конуса приближается к 45°. Таким образом, если взять безконечно-тонкий усеченный конус, то проведя производящую MS под углом 45° к оси, получим отсек MNPQ испытывающий меньшее сопротивление нежели PMRQ, при большем объеме, отсюда следует также, что сопротивление встречаемое коническою поверхностью MR больше суммы сопротивлений на коническую поверхность MN и на кольцевую площадь NR. Следовательно, если имеется какая-либо поверхность вращения, касательная к меридиану которой в какой-либо точке составляет с осью угол больше 45°, то взяв поверхность образованную вращением ломанной DMNRH, элемент MN которой составляет 45° с осью, получим тело, объем котораго больше нежели у первоначальнаго, сопротивление же меньше; значит, наименьшим сопротивлением будет обладать в этом случае такое тело, для котораго ни в одной точке вышеуказанной замены сделать нельзя, иначе у котораго касательная к меридиану составляет везде угол в 45°, и следовательно дуга меридиана MH заменена наклоненною к оси под углом 45° прямою и конечною ея ординатою.

© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... наибольшей ширине 164)

      Это утверждение Ньютона всецело относится к вариационному исчислению, и приведенный им ответ на вопрос о теле вращения представляющаго наименьшее сопротивление указывает, что им была решена первая задача в этой области, хотя он и не привел метода, которым это решение получено.

      К переводу Motte'a «Начал» на английский язык сделано небольшое прибавление, в котором, по словам переводчика, его друг дает решение задачи о теле наименьшаго сопротивления. Перевод этот издан в 1727–1729 годах, поэтому, приведенное решение может дать указания на то, каким образом решались подобные вопросы английскими математиками современниками Ньютона.

      Пусть BC есть ось вращения (фиг. 170b), B заданная на ней точка и BG также заданная крайняя ордината искомой кривой GD, которая своим обращением около оси BC должна образовать поверхность, испытывающую при движении вдоль оси CB наименьшее сопротивление.

      На оси BC берется произвольная точка M, и пусть MN есть ордината искомой кривой; возьмем безконечно близко к B точку b и безконечно близко к M точку m, так чтобы сумма $\displaystyle {\textstyle\frac{1}{2}}$Mm + $\displaystyle {\textstyle\frac{1}{2}}$Bb оставалась постоянной, какую бы точку M на оси ни брать; обозначим эту сумму через $ \varepsilon$, положим также $\displaystyle {\textstyle\frac{1}{2}}$Mm - $\displaystyle {\textstyle\frac{1}{2}}$Bb = $\displaystyle \xi$, итак:

$\displaystyle {\textstyle\frac{1}{2}}$Mm + $\displaystyle {\textstyle\frac{1}{2}}$Bb = $\displaystyle \varepsilon$;    $\displaystyle {\textstyle\frac{1}{2}}$Mm - $\displaystyle {\textstyle\frac{1}{2}}$Bb = $\displaystyle \xi$,
проведя ординаты mn и bg и прямыя N$ \nu$ и G$ \gamma$ параллельныя оси получим отрезочки $ \nu$n и $ \gamma$g, и будем выбирать длину $ \xi$, так чтобы было
$\displaystyle \nu$n = $\displaystyle \gamma$g = $\displaystyle \alpha$,
где $ \alpha$ также постоянная, т.-е, не зависит от положения точки M.

      Докажем сперва, что сумма сопротивлений испытываемых элементами поверхности происходящими от обращения отрезочков Gg и Nn будет наименьшая при условии:

Gg4 : Nn4 = BG . Bb : MN . Mm.

      Сопротивление испытываемое разсматриваемыми элементами поверхности по направлению BC пропорционально соответственно кольцевым площадям описанным отрезочками $ \nu$n и $ \gamma$g и обратно пропорционально Nn2 и Gg2, а так как эти кольцевыя площади пропорциональны ординатам MN и BG, ибо по условию $ \nu$n и $ \gamma$g постоянны, то сумма сопротивлений пропорциональна количеству

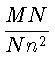$\displaystyle {\frac{BG}{Gg^2}}$ + $\displaystyle {\frac{MN}{Nn^2}}$;
это количество и должно быть наименьшим, причем BG и MN надо считать постоянными, а изменяются лишь Gg и Nn.

      Но

Gg2 = Bb2 + $\displaystyle \gamma$g2 = ($\displaystyle \varepsilon$ - $\displaystyle \xi$)2 + $\displaystyle \alpha^{2}_{}$;    Nn2 = mM2 + $\displaystyle \nu$n2 = ($\displaystyle \varepsilon$ + $\displaystyle \xi$)2 + $\displaystyle \alpha^{2}_{}$,
следовательно, наименьшею должна быть величина
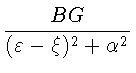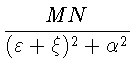$\displaystyle {\frac{BG}{(\varepsilon - \xi)^2 + \alpha^2}}$ + $\displaystyle {\frac{MN}{(\varepsilon + \xi)^2 + \alpha^2}}$,
уравнивая нулю ея производную по $ \xi$ имеем
$\displaystyle {\frac{BG \cdot (\varepsilon - \xi)}{[(\varepsilon - \xi)^2 + \alpha^2]^2}}$ = $\displaystyle {\frac{MN \cdot (\varepsilon + \xi)}{[(\varepsilon + \xi)^2 + \alpha^2]^2}}$
т.-е.
Gg4 : Nn4 = BG . Bb : MN . Mm.

      Но для крайней точки B, на основании предыдущей теоремы угол gGB должен равняться 135°, так что Gg = $ \sqrt{2}$$ \gamma$g, следовательно Gg4 = 4$ \gamma$g4 и предыдущая пропорция будет:

4$\displaystyle \gamma$g4 : Nn4 = BG . Bb : MN . Mm. (1)

      Проведя GR параллельно nN (т.-е. в пределе параллельно касательной в точке N), будем иметь подобные треугольники n$ \nu$N и BGR, из которых следует:

$\displaystyle \nu$n : $\displaystyle \nu$N = BG : BR
но
$\displaystyle \nu$n = g$\displaystyle \gamma$ = Bb  и   $\displaystyle \nu$N = Mm,
следовательно,
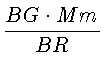Bb = $\displaystyle {\frac{BG \cdot Mm}{BR}}$.

      Вместе с тем

$\displaystyle \nu$n : Nn = BG : GR
значит:
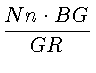
$\displaystyle \nu$n = $\displaystyle \gamma$g = $\displaystyle {\frac{Nn \cdot BG}{GR}}$
и из пропорции (1) следует:
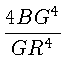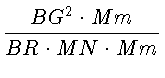
$\displaystyle {\frac{4BG^4}{GR^4}}$ = $\displaystyle {\frac{BG^2 \cdot Mm}{BR \cdot MN \cdot Mm}}$
или иначе:
4BG2 . BR : GR3 = GR : MN
это и есть данное в тексте условие.

      Примем ось вращения за ось x, и положим

MN = y,  BG = a,
тогда
tg GRB = y';  BR = $\displaystyle {\frac{a}{y'}}$
и
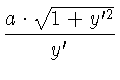
GR = $\displaystyle {\frac{a \cdot \sqrt{1 + y'^2}}{y'}}$
и предыдущее условие равносильно при теперешних обозначениях дифференциальному уравнению
$\displaystyle {\frac{yy'^3}{(1+y'^2)^2}}$ = $\displaystyle {\textstyle\frac{1}{4}}$a (2)

      Обозначая через k коэффициент сопротивления, получим, что полное сопротивление на поверхность выражается интегралом:

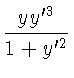k$\displaystyle \int\limits_{x_0}^{x}$$\displaystyle {\frac{yy'^3}{1+y'^2}}$ dx.

       Разыскание minimum'а этого интеграла, по правилам вариационного исчисления приводит к уравнению:

$\displaystyle {\frac{\partial F}{\partial y}}$ - $\displaystyle {\frac{d}{dx}}$ . $\displaystyle {\frac{\partial F}{\partial y'}}$ = 0 (3)
где
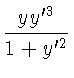
F = $\displaystyle {\frac{yy'^3}{1+y'^2}}$

       Но так как функция F переменной x явно не содержит то ея полная производная по x будет:

$\displaystyle {\frac{dF}{dx}}$ = $\displaystyle {\frac{\partial F}{\partial y}}$ . y' + $\displaystyle {\frac{\partial F}{\partial y'}}$ . y'',
это уравнение на основании предыдущаго напишется так:
$\displaystyle {\frac{dF}{dx}}$ - $\displaystyle \left(\vphantom{ y' \displaystyle\frac {d}{dx} \displaystyle\frac... ...al F}{\partial y''} + y'' \displaystyle\frac {\partial F}{\partial y'} }\right.$y'$\displaystyle {\frac{d}{dx}}$$\displaystyle {\frac{\partial F}{\partial y''}}$ + y''$\displaystyle {\frac{\partial F}{\partial y'}}$ $\displaystyle \left.\vphantom{ y' \displaystyle\frac {d}{dx} \displaystyle\frac... ...al F}{\partial y''} + y'' \displaystyle\frac {\partial F}{\partial y'} }\right)$ = 0
здесь первая часть есть полная производная по x и, значит, по интегрировании будет:
F - y'$\displaystyle {\frac{\partial F}{\partial y'}}$ = C (4)

       В разсматриваемом случае

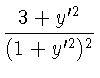$\displaystyle {\frac{\partial F}{\partial y'}}$ = yy'2 . $\displaystyle {\frac{3+y'^2}{(1+y'^2)^2}}$,
полагая
C = - $\displaystyle {\textstyle\frac{1}{2}}$a
и получаем Ньютоново решение
$\displaystyle {\frac{yy'^3}{(1+y'^2)^2}}$ = $\displaystyle {\textstyle\frac{1}{4}}$a (5)

       Ньютон не счел нужным представить свое решение в аналитической форме, т.-е. положив y' = p выразить в функции p не только ординату y

y = $\displaystyle {\textstyle\frac{1}{4}}$a . $\displaystyle {\frac{(1+p^2)^2}{p^3}}$ (6)
но и абсциссу x. Заметив, что dx =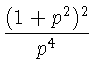 $\displaystyle {\frac{dy}{p}}$ имеем:
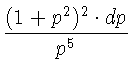x = $\displaystyle \int$$\displaystyle {\frac{dy}{p}}$ = $\displaystyle {\frac{y}{p}}$ + $\displaystyle \int$$\displaystyle {\frac{y \,dp}{p^2}}$ = $\displaystyle {\textstyle\frac{1}{4}}$a . $\displaystyle {\frac{(1+p^2)^2}{p^4}}$ + $\displaystyle {\textstyle\frac{1}{4}}$a$\displaystyle \int$$\displaystyle {\frac{(1+p^2)^2 \cdot dp}{p^5}}$ =
= $\displaystyle {\textstyle\frac{1}{4}}$a$\displaystyle \left[\vphantom{ \displaystyle\frac {3}{4}\cdot\displaystyle\frac {1}{p^4}+ \displaystyle\frac {1}{p^2}+\log p }\right.$$\displaystyle {\textstyle\frac{3}{4}}$ . $\displaystyle {\frac{1}{p^4}}$ + $\displaystyle {\frac{1}{p^2}}$ + log p$\displaystyle \left.\vphantom{ \displaystyle\frac {3}{4}\cdot\displaystyle\frac {1}{p^4}+ \displaystyle\frac {1}{p^2}+\log p }\right]$ + C1 (7)
где C1 постоянная произвольная, определяемая в разсматриваемом случае из условия, что при p = 1, x должно равняться x0.

© сканирование, верстка, IAGSoft (iagsoft@imm.uran.ru), 2000