Здесь опубликованы фрагменты книги:

Г.Г. Черный Течения газа с большой сверхзвуковой скоростью. М.: Физматгиз, 1959.
имеющие отношение к аэродинамической задаче Ньютона.

Г Л А В А   III


ЗАКОН СОПРОТИВЛЕНИЯ НЬЮТОНА;
МЕТОД КАСАТЕЛЬНЫХ КОНУСОВ (ИЛИ КЛИНЬЕВ);
ФОРМУЛА БУЗЕМАНА И МЕТОД ПОГРАНИЧНОГО СЛОЯ


§ 1. Закон сопротивления Ньютона


Практическая важность задачи об определении сил, действующих на тела при большой сверхзвуковой скорости, пробудила интерес к разработке методов расчета давления на поверхности движущихся с такой скоростью тел.

Хорошо разработанный метод линеаризации уравнений пригоден для расчета обтекания тонких тел только при малых значениях параметра подобия K. Этот метод подробно описан в ряде руководств по аэродинамике и не будет рассматриваться ниже.

В общем случае обтекания тел потоком с большой сверхзвуковой скоростью система соотношений, описывающих движение газа, допускает некоторые упрощения (гл. I, § 4 и гл. II, § 3), но тем не менее она продолжает оставаться сложной и трудно поддается решению.

При обтекании тел (толщину которых не обязательно считать малой) потоком с очень большой сверхзвуковой скоростью упрощаются лишь краевые условия на головной ударной волне (гл. I, § 4), что фактически не облегчает решения задачи по сравнению с общим случаем.

* * *

Для быстрых расчетов аэродинамических характеристик тел желательно иметь также простые формулы, пусть даже не обоснованные строго физическими или математическими соображениями, но хорошо аппроксимирующие более точные решения для распределения давления по поверхности тел того или иного класса. Такие простые формулы для давления дает закон сопротивления Ньютона; у заостренных впереди профилей или тел вращения давление на головной части может быть найдено, например, и по методу касательных клиньев или касательных конусов. Эти приближенные способы определения давления на поверхности тел при обтекании их потоком с большой сверхзвуковой скоростью также излагаются в настоящей главе.

Первая попытка определить, исходя из общих законов механики, сопротивление движению тел в газах и жидкостях принадлежит Ньютону [4].

Ньютон принимал, что среда, обтекающая тело, состоит из одинаковых частиц, расположенных на равных расстояниях друг от друга и не взаимодействующих между собой. При столкновении с элементом поверхности тела частицы изменяют нормальную к элементу составляющую своего количества движения, вследствие чего и возникает сила давления потока на тело.

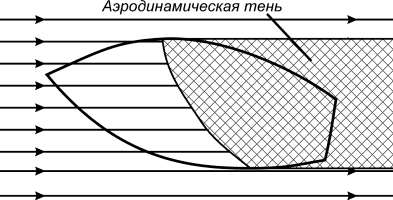
Согласно теории Ньютона давление на элемент поверхности тела зависит только от ориентации этого элемента по отношению к набегающему потоку частиц и не зависит от формы остальной части тела. Очевидно при этом, что сопротивление тела определяется только формой его головной части, поскольку только эта часть тела испытывает столкновения с частицами; теория Ньютона не дает возможности найти давление на участки поверхности тела, лежащие в его «аэродинамической тени» (рис. 3.1). Согласно этой теории давление на этих участках поверхности равно нулю.

Рис. 3.1. Обтекание тела согласно модели Ньютона.

Для определения величины давления потока частиц на тело согласно теории Ньютона рассмотрим элемент поверхности F, наклоненный под углом $ \alpha$ к направлению набегающего потока. Масса частиц, сталкивающихся с этим элементом поверхности в единицу времени, равна $ \rho$VF sin$ \alpha$, где $ \rho$ — плотность среды и V — скорость движения частиц. Сила, действующая в результате столкновений на элемент F, зависит от характера взаимодействия между частицами и поверхностью тела. При неупругом столкновении нормальная составляющая этой силы равна

$\displaystyle \rho$V2F sin2$\displaystyle \alpha$

так как количество движения единицы массы изменяется в нормальном к элементу поверхности направлении на величину V sin$ \alpha$. В этом случае давление, определяемое как отношение нормальной силы к площади, на которую эта сила действует, равно, следовательно,

p = $\displaystyle \rho$V2sin2$\displaystyle \alpha$

При неупругом столкновении с гладкой поверхностью частицы продолжают двигаться по инерции вдоль нее, сохранив при столкновении касательную к поверхности составляющую количества движения (поскольку движение частиц является инерциальным, то оно происходит с постоянной по величине скоростью вдоль геодезических линий поверхности).

Полученная Ньютоном формула в течение более двух столетий служила основой для расчета сопротивления движению тел в воздухе и для определения ветровых нагрузок на элементы строений, несмотря на то, что сам Ньютон высказывал сомнение относительно возможности применять к течениям реальных жидкостей выводы, полученные им для идеализированной среды. К тому же и опыты, проведенные при небольших скоростях течения жидкости вскоре после опубликования «Математических начал», не подтвердили формулу Ньютона [5].

Однако, как уже было отмечено в гл. I на частном примере пластины под углом атаки, при обтекании тел газом с очень большой сверхзвуковой скоростью картина течения близка к той, которая была принята Ньютоном в его теории при неупругом столкновении частиц с телом [5, 6, 7]. В этом случае ударная волна в головной части тела близка к его поверхности, так что возмущение, вносимое в поток телом, не распространяется вверх по потоку и частицы газа доходят почти до поверхности тела, не изменяя своей скорости, а затем после прохождения через ударную волну движутся в тонком слое между ударной волной и поверхностью тела.

* * *

§ 2. Использование формулы Ньютона для определения аэродинамических характеринстик тел и для нахождения тел с минимальным сопротивлением

Изложенные в предыдущем параграфе результаты дают основание заключить, что формула Ньютона может быть использована для определения аэродинамических характеристик клиновидных и конусовидных тел, а также тел, подобных изображенным на рисунках 3.5—3.8, при больших сверзвуковых скоростях в тех случаях, когда не требуется высокая точность.

* * *

Однако, несмотря на наличие значительного числа решений линеаризованных задач о телах наименьшего сопротивления в сверхзвуковом потоке, эти решения не могут быть использованы по причинам уже излагавшимся ранее, при больших сверхзвуковых скоростях. При таких скоростях для решения вариационной задачи нахождении тела минимального сопротивления может быть испольована формула Ньютона.

Первое решение такой задачи было дано самим Ньютоном [4]. Воспроизведем полученный им результат. Согласно формуле

p = $\displaystyle \rho_{1}^{}$V2sin2$\displaystyle \alpha$,

сила сопротивления, приложенная к участку длиной l поверхности профиля или тела вращения, равна

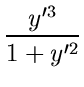X = $\displaystyle \rho_{1}^{}$V2$\displaystyle \int\limits_{0}^{l}$(2$\displaystyle \pi$y)$\scriptstyle \nu$ - 1$\displaystyle {\frac{y'^3}{1+y'^2}}$dx (3.3)

где $ \nu$ = 1 для плоского и $ \nu$ = 2 для осесимметричного течения. Это выражение позволяет решать различные задачи об определении формы тел с наименьшим сопротивлением. Рассмотрим, например, простейший случай, когда заданы координаты концов обтекаемого контура, т. е. y(0) = y0, y(l )= y1 (B плоском потоке всегда можно считать y0 = 0). Отыскание минимума выражения (3.3) для силы сопротивления приводится, как известно, к решению дифференциального уравнения

$\displaystyle {\frac{\partial F}{\partial y}}$ - $\displaystyle {\frac{d}{dx}}$$\displaystyle {\frac{\partial F}{\partial y'}}$ = 0 (3.4)

где F =  y$\scriptstyle \nu$ - 1$ {\frac{y'^3}{1+y'^2}}$. Так как функция F в рассматриваемом случае не содержит x явно, то

$\displaystyle {\frac{dF}{dx}}$ = $\displaystyle {\frac{\partial F}{\partial y}}$y' + $\displaystyle {\frac{\partial F}{\partial y'}}$y''

и в силу уравнения (3.4) получаем

0 = $\displaystyle {\frac{dF}{dx}}$ - $\displaystyle \left(\vphantom{ y' \frac{d}{dx} \frac{\partial F}{\partial y'} + y''\frac{\partial F}{\partial y'} }\right.$y'$\displaystyle {\frac{d}{dx}}$$\displaystyle {\frac{\partial F}{\partial y'}}$ + y''$\displaystyle {\frac{\partial F}{\partial y'}}$$\displaystyle \left.\vphantom{ y' \frac{d}{dx} \frac{\partial F}{\partial y'} + y''\frac{\partial F}{\partial y'} }\right)$ = $\displaystyle {\frac{dF}{dx}}$ - $\displaystyle {\frac{d}{dx}}$$\displaystyle \left(\vphantom{ y' \frac{\partial F}{\partial y'} }\right.$y'$\displaystyle {\frac{\partial F}{\partial y'}}$$\displaystyle \left.\vphantom{ y' \frac{\partial F}{\partial y'} }\right)$.

Отсюда после интегрирования находим интеграл этого уравнения

F - y'$\displaystyle {\frac{\partial F}{\partial y'}}$ = const,

который, после подстановки в него значений F и $ {\frac{\partial F}{\partial y'}}$, приобретает вид

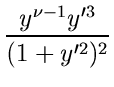$\displaystyle {\frac{y^{\nu-1}y'^3}{(1+y'^2)^2}}$ = const. (3.5)

Таким образом, в плоском потоке ($ \nu$ = 1) экстремали представляют собой прямые линии, так что телом наименьшего сопротивления в теории Ньютона, как и в линейной теории, является клин (в точной теории сверхзвуковых течений идеального газа этот результат несправедлив; см. гл. IV, § 4). В осесимметричном потоке ($ \nu$ = 2) уравнение экстремалей легко представить в параметрической форме, принимая за параметр величину p = y' — тангенс угла наклона элемента контура тела к направлению набегающего потока. Согласно равенству (3.5)

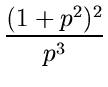y = C$\displaystyle {\frac{(1+p^2)^2}{p^3}}$.

Путем интегрирования соотношения dx = $ {\frac{dy(p)}{p}}$ получаем

x = C$\displaystyle \left(\vphantom{\frac{3}{4p^4}+\frac{1}{p^2}+\ln p }\right.$$\displaystyle {\frac{3}{4p^4}}$ + $\displaystyle {\frac{1}{p^2}}$ + ln p$\displaystyle \left.\vphantom{\frac{3}{4p^4}+\frac{1}{p^2}+\ln p }\right)$ + C1.

На рисунке 3.11 представлена в виде кривой зависимость y от x, определяемая этими формулами.
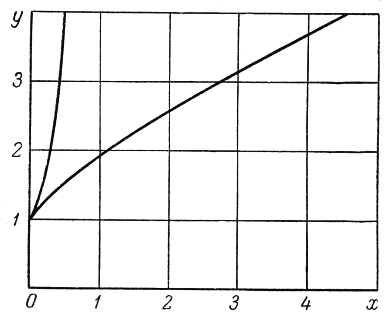Рис. 3.11. Образующая тела вращения, обладающего минимальным сопротивлением при вычислении давления по формуле Ньютона.
Кривая имеет точку возврата при p = $ \sqrt{3}$; масштабные постоянные C и C1 в выражениях для y и x выбраны при построении кривой так, чтобы точка возврата совпадала с точкой x = 0, y = 1 (ветвь кривой с большими значениями p должна использоваться при нахождении формы тел с малым удлинением). Обозначим через YH(p) и XH(p) зависимости y и x от p, соответствующие сделанному выбору постоянных. Тогда, если считать длину тела равной единице, то форма образующей тела с минимальным сопротивлением при заданных y0 и y1 определится выражениями

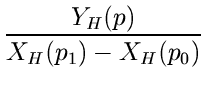y = $\displaystyle {\frac{Y_H(p)}{X_H(p_1) - X_H(p_0)}}$,

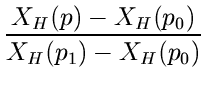x = $\displaystyle {\frac{X_H(p)-X_H(p_0)}{X_H(p_1) - X_H(p_0)}}$,

где p0 и p1 связаны с y0 и y1 очевидными соотношениями

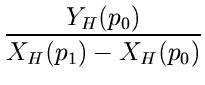y0 = $\displaystyle {\frac{Y_H(p_0)}{X_H(p_1) - X_H(p_0)}}$,

y1 = $\displaystyle {\frac{Y_H(p_1)}{X_H(p_1) - X_H(p_0)}}$,

Решение Ньютона использовано для изучения свойств тела с минимальным сопротивлением при большой сверхзвуковой скорости в работе [19].


ЛИТЕРАТУРА

4. И. Н ь ю т о н,  Математические начала натуральной философии, Собр. трудов А. Н. Крылова, т. 7, Изд. АН СССР, М.–Л., 1936.
5. Th. K a r m a n,  Isaac Newton and aerodynamics, Journ. Aeron. Sci., 9, 14 (1942).
6. P. S. E p s t e i n,  On the air resistance of projectiles, Proc. Nat. Acad. Sci. USA, 17, 9 (1931).
7. A. F. Z a h m,  Superaerodynamics, Jorn. Franklin Inst., 217, 2 (1934).
19. Г. Л. Г р о д з о в с к и й,  Некоторые особенности обтекания тел при больших сверхзвуковых скоростях, Изв. АН СССР, ОТН, 6 (1957).



Vari Home
Вариационное исчисление | Домашняя страница


Пишите по адресу: iagsoft@imm.uran.ru