Задача о брахистохроне

Найдем кривую, соединяющую две точки, при движении вдоль которой частица из состояния покоя под действием гравитации двигалась бы за наименьшее время. Из закона сохранения энергии,

таким образом

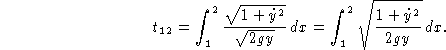
Варьируемая функция в таком случае

и уравнение Эйлера-Лагранжа дает

где

Пусть

Положим

тогда

Если учитывается трение скольжения, то должны присутствовать члены, соответствующие нормальной компоненте веса и нормальной компоненте ускорения (возникающей из-за кривизны траектории). Включение обоих членов требует применения техники сдержанных вариаций (a constrained variational technique) (Ashby et al. 1975), но включение только нормальной компоненты веса позволяет получить элементарное решение.

Тангенциальный и нормальный вектора есть

Гравитация и трение выражаются

а компоненты вдоль кривой есть

второй^* закон Ньютона дает

Но

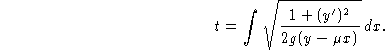
Используя уравнение Эйлера-Лагранжа, получим

Это можно сократить до

Положим

решение есть

Литература

Ashby, N.; Brittin, W.E.; Love, W.F.; and Wyss, W. "Brachistochrone with Coulomb Friction." Amer. J. Phys. 43, 902-905, 1975.

^* Примечание переводчика