Feedback: mail Eric Home: Eric's Home Page

Brachistochrone Problem

 

Find the curve joining two points along which a particle falling from rest accelerated by gravity travels in the least time. From conservation of Energy,

so

The function to be varied is then

and the Euler-Lagrange Differential Equation gives

where

Let

Now let

then

If Kinetic Friction is included, terms corresponding to the normal component of weight and the normal component of the acceleration (present because of path curvature) must be included. Including both terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight only gives an elementary solution. The tangent and normal vectors are

Gravity and friction are then

and the components along the curve are

so Newton's First Law gives

But

so

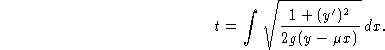
Using the Euler-Lagrange Differential Equation gives

This can be reduced to

Now letting

the solution is

References

Ashby, N.; Brittin, W.E.; Love, W.F.; and Wyss, W. ``Brachistochrone with Coulomb Friction.'' Amer. J. Phys. 43, 902-905, 1975.

Haws, L. and Kiser, T. ``Exploring the Brachistochrone Problem.'' Amer. Math. Monthly 102, 328-336, 1995.

This document is mirror from www.astro.virginia.edu on home.imm.uran.ru (Ekaterinburg, Russia).
Original URL: http://www.astro.virginia.edu/~eww6n/physics/BrachistochroneProblem.html. There is the Russian version. Brachistochrone applet