SOFTWARE FOR THE COURSE OF CALCULUS OF VARIATIONS

1. AERODYNAMIC NEWTON'S PROBLEM (ANP)

The problem consists of searching the generating line y(x) of a rotation-body with the minimum resistance in a flow of rarefied ideal gas (Newton, 1916; Tikhomirov, 1990). The gas is represented as collection of infinitely small particles which do not mutually collide and are mirror-like reflected having collided with the body. At first, we solve the problem, following (Krasnov, et al., 1973), under assumption that the value of y'² is small. It is shown, that this assumption isn't fulfilled on optimal solution. After that, the numerical search of the solution in the class of functions y=x^p is demonstrated (Fig. 1). Further, in frames of the numerical approach, the program for finding the solution by the Euler method (as a piecewise linear approximation) is demonstrated. Here, the problem is reduced to searching the minimum of the function of many variables. To minimize this function, we use one technique of direct search. This technique is described in (Bunday, 1984) as the Hooke-Jeeves method. The optimal solution has a corner point (Newton, 1916) (Fig. 2).

Fig. 1. Dependence of the drag coefficient upon the parameter p (i.e., the class of functions y=x^p). The sections of the rotation body for certain are given in the upper part.

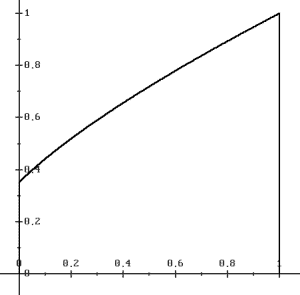Fig. 2. Optimal solution for ANP

2. PROBLEM OF THE MINIMUM
ROTATION-SURFACE (PMRS)

It is necessary to find a generating line of the rotation-surface with minimum area. It is known that the line to be found is a catenary. Depending on the concrete boundary conditions, there can exist either two solutions of the Euler equation or alone or none (Fig. 3). These solutions are catenaries. In traditional courses, one does not pay attention enough to the case of absence of the classic solution. In the numerical solution by the Euler method, the broken-wise solution is easily discovered. These are two disks for which the generating line consists of two vertical segments and a horizontal one lying on the axis of rotation. Moreover, the broken-wise solution can be a global minimum in the zone of existing the solution for the Euler equation (Ahiezer, 1955; Young, 1969; Cesari, 1983). If the left-end point is fixed at (0, 1), then one can construct a partition of the quadrant of feasible locations for the right-end point. If the right-end point is located in the area I (see Fig. 4), then the global minimum is a catenary. If this point is in the area II, then the global minimum is a broken-wise solution (disks) while the catenary gives only a local minimum. If the point is in the area III, then the only (global) minimum is the broken-wise solution, no solutions of the Euler equation exist. These facts can be found in (Anisimov, 1904; Ahiezer, 1955; Young, 1969; Cesari, 1983), however, they are not widely known.

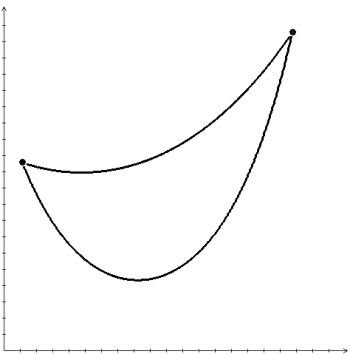Fig. 3. Two solutions of the Euler equation for PMRS

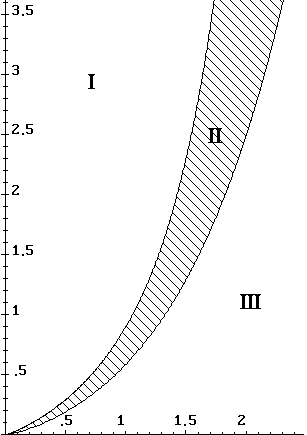Fig. 4. Minimum existence depending on location of the right-end point:
I - catenary is a global minimum
II - catenatry is a local minimum only, disks are a global minimum
III - disks are the only global minimum

3. BRACHISTOCHRONE PROBLEM (BP)

In this problem, it is necessary to find the line of fastest descent between two points in the vertical plane (Bernoulli, 1937; Tikhomirov, 1990). This line is an arc of the cycloid. The problem of finding the concrete cycloid for given boundary conditions is usually out of the frame of study. For arbitrary feasible boundary conditions, the program has been elaborated which finds and visually represents the optimal solution both in the form of the cycloid and in the class of two-link piecewise lines. The motion of a point along both the trajectories is animated. An Java-version of this program for Internet is also elaborated (see at http://home.ural.ru/~iagsoft/BrachJ.html).

For the case of motion in the central gravity field (BPCGF), the brachistochrone is calculated by the Euler method. For this case, the optimal solution (Fig. 6) and isochrones (Fig. 7) obtained on the multiprocessor system (Ivanov, 1995) are demonstrated. Here the "isochrone" means a line consisting of points with the same optimal time. In Fig. 6 the center of gravitation is at (0, 0), the starting point is (1, 0), optimal trajectories are given for certain endpoints having norm ||(x₁, y₁)|| = 1.

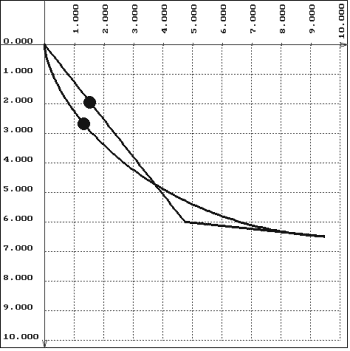Fig. 5. Optimal solutions of BP for two class of lines

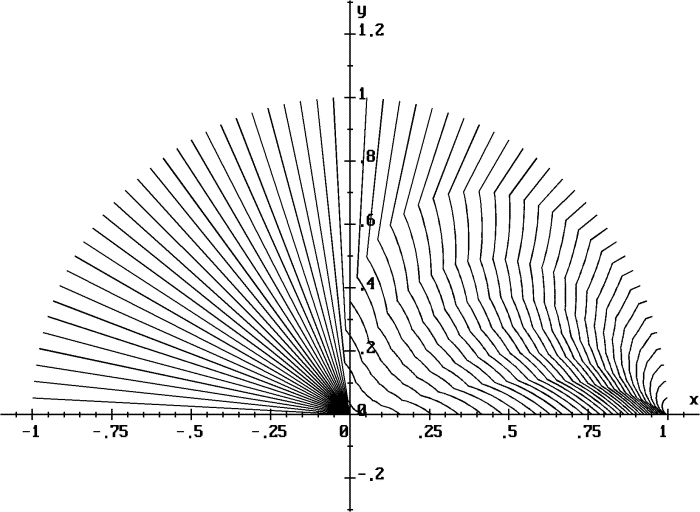Fig. 6. Field of optimal trajectories for BPCGF

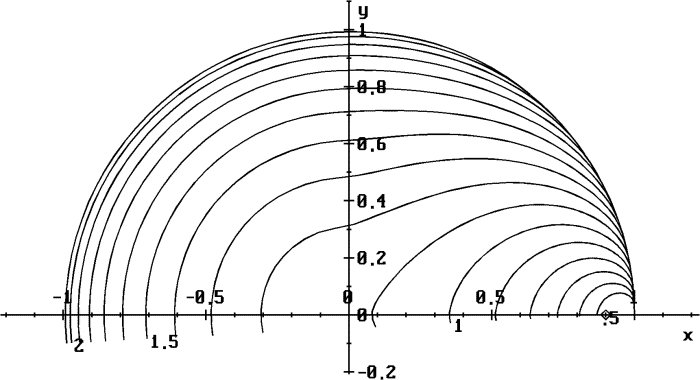Fig. 7. Isochrones for BPCGF. The center of gravitation is at (0, 0), the starting point is (1, 0).

ACKNOWLEDGEMENT

This work was supported by the Russian Foundation of Basic Researches under Grant No. 97-01-00458.

REFERENCES

Ahiezer, N.I. (1955). Lectures on the calculus of variations. TehGIZ, Moscow [in Russian].

Anisimov, V. (1904). Course on the calculus of variations. V. I, Warshaw [in Russian].

Bernoulli, J. (1937). Selected works on mechanics. TehGIZ, Moscow, Leningrad [in Russian].

Bunday, B. (1984). Basic optimisation methods. Edward Arnold, London.

Cesari, L. (1983) Optimization Theory and Applications Problems with Ordinary Differential Equations. Springer-Verlag, N.Y., Heidelberg, Berlin.

Ivanov, A.G. (1995). An Experience of Level Line Constructions on Transputer Systems. In: Algoritmy i Programmnye Sredstva Parallel'nykh Vychislenii (Algorithms and Program Means of Parallel Computations) (Kukushkin A.P. and S.V. Sharf, (Eds.)), 69-78. Ural Branch of Russian Academy of Sciences, Ekaterinburg [in Russian].

Krasnov, M.A., G.I. Makarenko and A.I. Kiselev (1973). Calculus of Variations. Nauka, Moscow [in Russian].

Newton, I. (1916). Philosophiae Naturalis Principia Mathematica. S.-Petersburg [in Russian].

Tikhomirov, V.M. (1990). Stories about Maxima and Minima. Translated from the Russian by Abe Shenitzer, Amer. Math. Soc. and Math. Assoc. of America.

Young, L.C. (1969). Lectures on the calculus of variations and optimal control theory. W.B. Saunders Co., Philadelphia, London, Toronto.