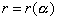Иванов А.Г. (Екатеринбург)
ЗАДАЧА О БРАХИСТОХРОНЕ В ЦЕНТРАЛЬНОМ ПОЛЕ ТЯГОТЕНИЯ1

Рассматривается задача о линии наискорейшего спуска в центральном поле тяготения. Предполагается, что центр тяготения находится в точке (0,0), сила тяготения обратно пропорциональна квадрату расстояния до центра тяготения. Удобно рассматривать движение в полярной системе координат с центром в (0,0). Время спуска по кривой, определяемой функцией 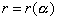r = r(/alpha), можно записать в виде

.

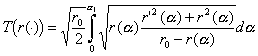Здесь постоянная всемирного тяготения и массы тел взяты равными единице.

При нахождении минимума функционала используется метод Эйлера [1] -- приближение искомой кривой кусочно-линейной ломаной. Таким образом, задача сводится к нахождению минимума функции многих переменных. Минимизация проводится с помощью метода Хука-Дживса [2]. Численный эксперимент показал, что в зависимости от граничных условий, локальный минимум достигается на двух решениях: решении, проходящем вдали от центра тяготения, и решении, проходящем через центр тяготения.

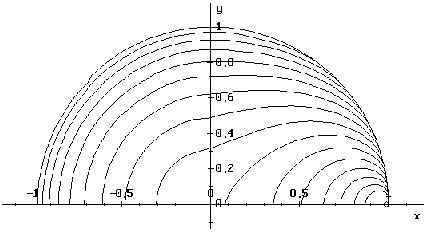
В рассматриваемой постановке определенный интерес представляет следующее исследование -- как изменяется время спуска по оптимальной траектории при изменении конечной точки, при этом начальная точка фиксируется. На рисунке изображены изохроны -- линии уровня времени оптимального спуска. Для нахождения изохрон использовалась параллельная программа [3].

Select for zooming of this figure
Изохроны в центральном поле тяготения. Время от 0.5 до 2.0, шаг 0.2

1. Л.Э.Эльсгольц. Вариационное исчисление. М.: Техгиз, 1958.

2. Б.Банди. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.

3. А.Г.Иванов. Опыт построения линий уровня на транспьютерных системах // Алгоритмы и программные средства параллельных вычислений: [Сб. науч.тр.]. Екатеринбург: УрО РАН, 1995.

1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (97-01-00458).
Пишите по адресу: iagsoft@imm.uran.ru