Уральское отделение Российской академии наук
Институт математики и механики
Алгоритмы и программные средства параллельных
вычислений -- 1999. Вып. 3




ПРИМЕНЕНИЕ ПАРАЛЛЕЛЬНОЙ
ПРОГРАММЫ ПОИСКА МИНИМУМА
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
К ЗАДАЧЕ О БРАХИСТОХРОНЕ
В ЦЕНТРАЛЬНОМ ПОЛЕ ТЯГОТЕНИЯ*

А.Г. Иванов

Описывается продолжение работ по созданию программы поиска минимума скалярной функции многих переменных [1]. Изложен опыт применения программы для решения нетрадиционной задачи о брахистохроне -- движение в центральном поле тяготения. Приведены результаты усовершенствования программы -- внедрение элементов метода случайного поиска, что является непосредственным продолжением предыдущей статьи [1].

1. Задача о брахистохроне в центральном поле

Задача о брахистохроне в центральном поле тяготения, физические модели которой описаны в п. 1 .1, не поддается решению аналитическими методами вариационного исчисления. В п. 1 .3 приведены результаты, полученные при помощи вычислений на МВС-100. Применение традиционной вычислительной техники не позволило бы провести вычисления с такой же точностью за приемлемое время.

1.1. Варианты содержательной постановки задачи

Одно из возможных обобщений традиционной задачи о брахистохроне [2,3] состоит в следующем. Постоянная сила тяжести заменяется на центральную силу, подчиняющуюся закону притяжения Ньютона: сила притяжения по величине обратно пропорциональна квадрату расстояния между притягивающимися телами и направлена по прямой, соединяющей центры этих тел. Тело -- центр притяжения -- жестко фиксируется в пространстве (для удобства центр тела помещается в начало координат). Задача формулируется следующим образом: Для двух данных точек найти кривую, соединяющую эти точки, такую, чтобы тяжелая материальная точка, выпущенная из "дальней" (по отношению к центру тяготения) точки с нулевой начальной скоростью, двигаясь по этой кривой, достигала бы "ближней" точки за минимально возможное время.

Недостаток приведенной формулировки в том, что при использовании терминов гравитации перед читателем мысленно возникают "космические" проблемы, что для этой задачи было бы неверно. Обыкновенный способ перемещения космических аппаратов ни в коей мере не напоминает движение по "рельсам", проложенным в космическом пространстве.

Другая трактовка, возможно, менее склонна ввести читателя в заблуждение. Представим себе движение электрических зарядов. В горизонтальной плоскости неподвижно закреплен положительный заряд. Заданы две точки -- начальная и конечная. Необходимо найти оптимальную траекторию массивного отрицательного заряда, двигающегося под действием силы, вызванной электростатическим притяжением к положительному заряду. Трением и электродинамическими эффектами пренебрегаем.

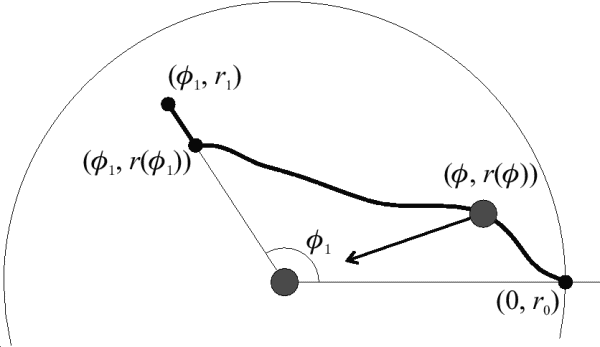
1.2. Формализация задачи. Функционал времени спуска

Рис. 1. Движение точки под действием центральной силы тяготения

Специфика поля тяготения подсказывает проводить выкладки в полярной системе координат с центром, совпадающим с центром тяготения (рис. 1). Пусть $ \phi$ - азимут (полярный угол), r - полярный радиус. Для упрощения выкладок гравитационную постоянную и массы тел предполагаем равными единице. Тогда сила, действующая на точку, по абсолютной величине равна

| F($\displaystyle \phi$, r)| = $\displaystyle {\frac{1}{r^2}}$ .

Если траектория движения задается графиком функции r = r($ \phi$), то время спуска можно вычислить, используя функционал

T(r( . )) = $\displaystyle \sqrt{\frac{r_0}{2}}$$\displaystyle \int\limits_{\phi_0}^{\phi_1}$$\displaystyle \sqrt{r(\phi)\frac{r'^2(\phi)+r^2(\phi)}{r_0-r(\phi)}}$ d$\displaystyle \phi$ . (1)

Если мы используем приведенный выше функционал для поиска оптимального решения, то "за бортом" нашего рассмотрения оказываются траектории с вертикальными участками, т.е. траектории, в которых есть участки лучей, выходящих из центра тяготения. Опыт решения подобных задач показывает, что для получения адекватного решения, как правило, необходимо введение вертикальных участков, по крайней мере, у граничных точек, т.е. на концах промежутка интегрирования (например участок между точками ($ \phi_{1}^{}$, r($ \phi_{1}^{}$)) и ($ \phi_{1}^{}$, r1) на рис. 1). В этом случае к функционалу (1) надо добавить время движения по вертикальным участкам:

T = $\displaystyle \sqrt{\frac{r_0}{2}}$$\displaystyle \int\limits_{\phi_0}^{\phi_1}$$\displaystyle \sqrt{r(\phi)\frac{r'^2(\phi)+r^2(\phi)}{r_0-r(\phi)}}$ d$\displaystyle \phi$ + V(r($\displaystyle \phi_{0}^{}$), r($\displaystyle \phi_{1}^{}$), r0, r1) , (2)

V(r($\displaystyle \phi_{0}^{}$), r($\displaystyle \phi_{1}^{}$), r0, r1) =  

  = | g(r0, r0) - g(r($\displaystyle \phi_{0}^{}$), r0)| + | g(r1, r0) - g(r($\displaystyle \phi_{1}^{}$), r0)| ,

где

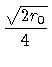
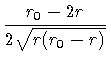
g(r, r0) = - $\displaystyle {\frac{\sqrt{2 r_0}}{4}}$$\displaystyle \left(\vphantom{ 2 \sqrt{r (r_0-r)}+r_0 \, \mbox{arctg} \left(\frac{r_0 - 2 r}{2 \sqrt{r (r_0-r)}} \right) }\right.$2$\displaystyle \sqrt{r (r_0-r)}$ + r0 arctg$\displaystyle \left(\vphantom{\frac{r_0 - 2 r}{2 \sqrt{r (r_0-r)}} }\right.$$\displaystyle {\frac{r_0 - 2 r}{2 \sqrt{r (r_0-r)}}}$ $\displaystyle \left.\vphantom{\frac{r_0 - 2 r}{2 \sqrt{r (r_0-r)}} }\right)$ $\displaystyle \left.\vphantom{ 2 \sqrt{r (r_0-r)}+r_0 \, \mbox{arctg} \left(\frac{r_0 - 2 r}{2 \sqrt{r (r_0-r)}} \right) }\right)$ .

При этом существуют пределы:

$\displaystyle \lim\limits_{r \to r_0}^{}$g(r, r0) = $\displaystyle {\frac{\sqrt{2}}{8}}$ r01.5 ,      g(r, r0) = - $\displaystyle {\frac{\sqrt{2}}{8}}$r01.5

При нахождении минимума функционала применяем метод Эйлера [2] -- приближение искомой кривой кусочно-линейной ломаной. Тем самым задача сводится к нахождению минимума функции многих переменных. Следует отметить, что функционал (1) не удается аналитически проинтегрировать даже на участках линейности функции r($ \phi$), что заставляет прибегать к численному интегрированию и значительно увеличивает время вычислений. Поэтому для решения задачи используем параллельную программу, описанную в  [1].

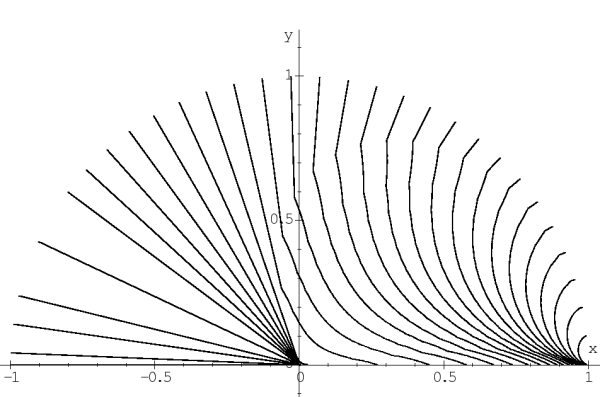Рис. 2. Поле оптимальных траекторий

1.3. Результаты вычислений

Для задачи о брахистохроне в центральном поле тяготения получено поле оптимальных траекторий (рис. 2). Здесь центр тяготения имеет координаты (0, 0), начальная точка для всех траекторий -- (1, 0). Изображены оптимальные траектории с конечными точками, имеющими полярный радиус r1 = 1 и различные полярные углы $ \phi_{1}^{}$.

Наличие поля оптимальных траекторий, рассчитанного с хорошей точностью, позволило улучшить точность построения линий уровня оптимального результата -- изохрон (рис. 3) по сравнению со случаем, когда изохроны строились на основе лишь значений функции оптимального результата [4].


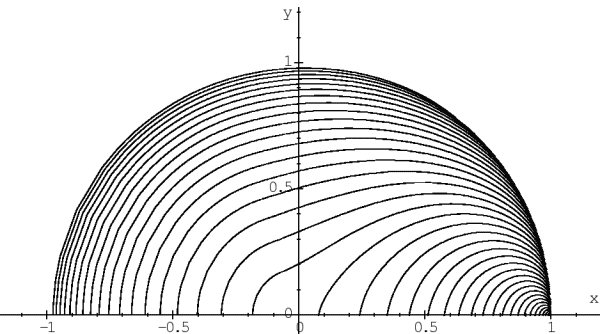Рис. 3. Изохроны в задаче о брахистохроне в центральном поле тяготения



2. Метод Монте-Карло в задаче поиска минимума

Этот раздел описывает усовершенствования, внесенные в параллельную программу поиска минимума, основной алгоритм которой изложен в статье [1]. Там же описаны используемые ниже понятия и термины.


2.1. Реализация

При работе задачи-мастера в конце очередного поиска вокруг базовой точки наступает период, когда мастер не занимается ``полезными" вычислениями, а выполняет цикл опроса рабочих. Этот цикл, в зависимости от конкретной задачи, может составлять довольно значительное время. Возникает мысль ``нагрузить" мастера какими-то полезными вычислениями. Очевидно, что попытки заставить мастера дублировать отстающих рабочих приведут (в естественных случаях1) к значительному увеличению времени счета. Таким образом, имеет смысл поручать мастеру обсчитывать на этом этапе лишь отдельные точки. При этом в существующий алгоритм легко интегрируются элементы метода Монте-Карло.

Опишем подробно реализацию метода Монте-Карло в рассматриваемой программе.

Во время цикла опроса рабочих (на этапе поиска вокруг базовой точки), когда для мастера нет точек для счета согласно основному алгоритму, мастер обсчитывает точки, сформированные случайно. Фрагмент программы, отвечающий за формирование случайной точки, выглядит следующим образом: 


tmp = 0;
for (i = 0; i < n; i++)
 {
  okl[i] = h*(1000.0-(rand()%2000))/1000.0;
  if (flag != 0 && tmp < fabs(okl[i]))
    tmp = fabs(okl[i]);
 }
if (flag != 0)
 {
  tmp = h / tmp;
  for (i = 0; i < n; i++) okl[i] *= tmp;
 }
for (i = 0; i < n; i++) okl[i] += baza[i];
где baza[] - массив координат базовой точки, okl[] - массив координат случайной точки, h - текущий шаг поиска, rand() - стандартная функция, выдающая псевдослучайное целое число, flag - флаг метода выбора точки.

Если значение переменной flag равно нулю, то будет сгенерирована случайная точка внутри гиперкуба со стороной 2h и с центром в текущей базовой точке. Если же flag отличен от нуля, то будет сгенерирована точка на границе упомянутого гиперкуба.

После вычисления значения функции в случайной точке результаты обрабатываются аналогично точкам основного алгоритма. Рассматривался следующий вариант алгоритма (в случае flag = 0): если при поиске вокруг базовой точки минимум найден в случайной точке, то происходит корректировка (уменьшение) текущего шага. Численный эксперимент показал неэффективность такого подхода.

В другой модификации алгоритма происходит отказ от работы со случайными точками "в конце поиска вокруг базовой точки", когда больше половины рабочих уже послали свои результаты мастеру и находятся в режиме ожидания. В такой момент естественно ожидать, что и остальные рабочие "в скором времени" пришлют пакеты с результатами. В этом случае мастеру выгоднее, "не отвлекаясь" на вычисление случайных точек, заниматься ожиданием приема.

2.2. Результаты применения

Применение метода Монте-Карло для наиболее переборного варианта (алгоритм 3) из описанных в [1] вариантов основного алгоритма не дало существенных изменений при счете. При этом незначительно (на несколько процентов) увеличилось время счета.

Для алгоритма 2 (см. [1]) анализ времени счета различных вариантов применения метода Монте-Карло представлен на рис. 4, 5. Здесь в качестве примера для тестирования изменений в алгоритме использовались вычисления одной траектории в задаче о брахистохроне в центральном поле тяготения. Во всех случаях решалась одна и та же задача, менялись только алгоритмы и число задействованных процессоров.

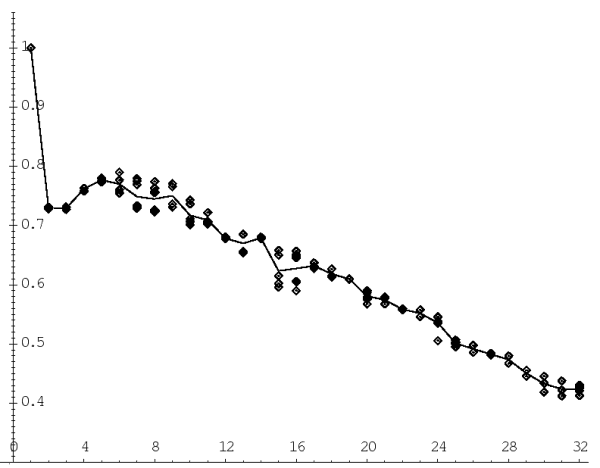Рис. 4. Эффективность распараллеливания Ef для варианта программы без метода Монте-Карло. Ось абсцисс -- число процессоров, ось ординат -- эффективность распараллеливания

На рис. 4 показана эффективность распараллеливания для алгоритма 2 без применения метода Монте-Карло. Эффективность распараллеливания Efn на n процессорах вычисляется по формуле Efn = t1/(ntn), где tn - время счета на n процессорах. Абсолютному распараллеливанию соответствует Efn = 1. Маркерами отмечены результаты отдельных запусков программы, сплошная линия -- среднее значение Efn. Видно, что даже без использования метода Монте-Карло время выполнения меняется от запуска к запуску. Это является, в частности, результатом разной загрузки процессорной сети и хост-машины iaglacisiaggold другими задачами в различные моменты.

На рис. 5 представлен аналогичный график для варианта алгоритма с применением метода Монте-Карло (ММК). Виден значительный, по сравнению с рис. 4, разброс времени выполнения при разных запусках с одним и тем же числом процессоров. На рис. 5 можно заметить, что в отдельных запусках были получены значения времени, близкие к абсолютному распараллеливанию.

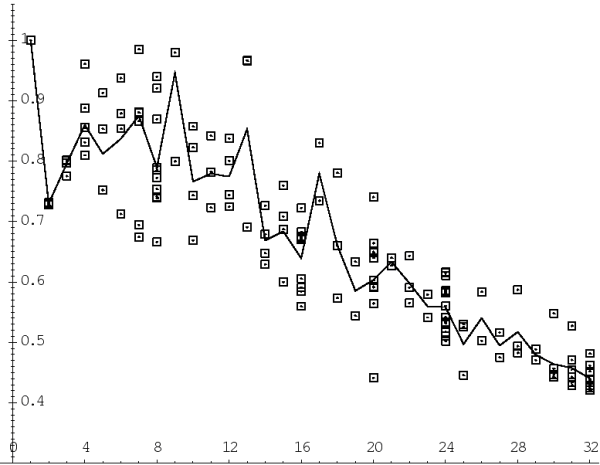Рис. 5. Эффективность распараллеливания Ef при применении метода Монте-Карло, flag=0 (ММК0)

Для проведения анализа преимуществ и недостатков различных вариантов применения ММК введем следующую величину (обобщенное время выполнения):

$\displaystyle \widetilde{T}$ = $\displaystyle {\frac{T_n}{T^*_n}}$ .

Здесь Tn - реальное время счета (однократного запуска) на n процессорах, T*n - среднее временя счета на том же числе процессоров для базового варианта программы (без применения ММК).

Величина $ \widetilde{T}$ характеризует преимущество ( $ \widetilde{T}$ < 1) или недостаток ( $ \widetilde{T}$ > 1) конкретного запуска варианта программы по сравнению со средним значением, полученным для "канонического" варианта (T*n).

Для анализа преимущества различных вариантов ММК будем использовать статистические характеристики обобщенного времени выполнения $ \widetilde{T}$, полученные при серии запусков программы на разном числе процессоров.


Т а б л и ц а 1
Оценка эффективности для NCPU $ \in$ [1, 32]
параметр   норма     ММК0     ММК4     ММК8  
N 136 150 119 261
$ \overline{\widetilde{T}}$ 1 0.935 0.922 0.955
$ \widetilde{T}_{\min}^{}$ 0.947 0.655 0.765 0.712
$ \widetilde{T}_{\max}^{}$ 1.064 1.316 1.173 1.117
$ \sigma_{\widetilde{T}}^{}$ 0.0206 0.0980 0.0852 0.0789
$ \overline{\widetilde{T}}$ - $ \sigma_{\widetilde{T}}^{}$ 0.979 0.837 0.837 0.876
$ \overline{\widetilde{T}}$ + $ \sigma_{\widetilde{T}}^{}$ 1.021 1.033 1.007 1.034

Произведя некоторое количество запусков задачи на различном числе процессоров, получим ряд значений $ \widetilde{T}$. На основе анализа статистических характеристик $ \widetilde{T}$ можно сделать выводы о преимуществе того или иного метода.

Рассчитываются следующие характеристики: средняя величина (математическое ожидание) $ \overline{\widetilde{T}}$, минимальное ( $ \widetilde{T}_{\min}^{}$) и максимальное ( $ \widetilde{T}_{\max}^{}$) значения, среднеквадратичное отклонение $ \sigma_{\widetilde{T}}^{}$, нижняя $ \overline{\widetilde{T}}$ - $ \sigma_{\widetilde{T}}^{}$ и верхняя $ \overline{\widetilde{T}}$ + $ \sigma_{\widetilde{T}}^{}$ границы наиболее вероятного интервала. Нас будет больше всего интересовать величина $ \overline{\widetilde{T}}$ + $ \sigma_{\widetilde{T}}^{}$. Если значение верхней границы наиболее вероятного интервала обобщенного времени для испытуемого метода окажется меньше, чем для образцового метода, будем считать, что испытуемый метод лучше, чем образцовый.


Т а б л и ц а 2
Оценка эффективности для NCPU $ \in$ [2, 16]
параметр   норма     ММК0     ММК4     ММК8  
N 81 80 62 133
$ \overline{\widetilde{T}}$ 1 0.922 0.922 0.934
$ \widetilde{T}_{\min}^{}$ 0.947 0.655 0.765 0.712
$ \widetilde{T}_{\max}^{}$ 1.064 1.120 1.173 1.117
$ \sigma_{\widetilde{T}}^{}$ 0.0236 0.1058 0.1002 0.0959
$ \overline{\widetilde{T}}$ - $ \sigma_{\widetilde{T}}^{}$ 0.976 0.817 0.822 0.838
$ \overline{\widetilde{T}}$ + $ \sigma_{\widetilde{T}}^{}$ 1.024 1.028 1.022 1.029

В табл. 1 - 3 показаны результаты статистической обработки обобщенного времени выполнения для алгоритма без применения ММК (норма) и различных вариантов алгоритма с применением ММК. Буква N обозначает число запусков, NCPU - число процессоров. Другие обозначения:

ММК0 -
базовый алгоритм с ММК:   flag = 0 (см. п. 2.1);
ММК4 -
алгоритм ММК с точками на границе гиперкуба:
flag $ \neq$ 0;
ММК8 -
модификация базового алгоритма ММК ( flag = 0), где мы отказываемся от работы со случайными точками "в конце поиска вокруг базовой точки".

Как видно из табл. 1, наилучшие результаты для общего случая (число процессоров 1 - 32) дает метод ММК4 (число, выделенное в последней строке таблицы жирным шрифтом, меньше, чем число, выделенное курсивом). Для малого числа процессоров (табл. 3) преимущество переходит к методу ММК8.


Т а б л и ц а 3
Оценка эффективности для NCPU $ \in$ [1, 8]
парметр   норма     ММК0     ММК4     ММК8  
N 42 46 36 72
$ \overline{\widetilde{T}}$ 1 0.926 0.938 0.916
$ \widetilde{T}_{\min}^{}$ 0.961 0.655 0.765 0.712
$ \widetilde{T}_{\max}^{}$ 1.030 1.118 1.145 1.112
$ \sigma_{\widetilde{T}}^{}$ 0.0190 0.1015 0.1041 0.0970
$ \overline{\widetilde{T}}$ - $ \sigma_{\widetilde{T}}^{}$ 0.981 0.824 0.834 0.819
$ \overline{\widetilde{T}}$ + $ \sigma_{\widetilde{T}}^{}$ 1.019 1.027 1.042 1.013

К моменту написания статьи не был исследован алгоритм, объединяющий ММК4 и ММК8, -- с точками на границе гиперкуба и с прекращением работы со случайными точками "в конце поиска вокруг базовой точки". Вполне возможно, что подобная модификация является наиболее подходящей.

СПИСОК ЛИТЕРАТУРЫ

1. Иванов А.Г. Параллельный алгоритм прямого поиска минимума функции многих переменных2// Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр. Вып. 2.]. Екатеринбург, 1998. С. 110-122.
2. Эльсгольц Л.Э. Вариационное исчисление. М.: Техгиз, 1958.
3. Янг Л. Лекции по вариационному исчислению и теории оптимального управления. М.: Мир, 1974.
4. Иванов А.Г. Задача о брахистохроне в центральном поле тяготения3// Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр. Вып. 2.]. Екатеринбург, 1998. C. 95-109.
5. Лацис А.O. Операционная среда ROUTER для транспьютерных систем. Документация по МВС-100.
6. Игумнов А.С., Коновалов А.В., Самофалов В.В., Шарф С.В. Развитие и адаптация системного программного обеспечения МВС-100 // Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр. Вып. 2.]. Екатеринбург, 1998. C. 123-133.
7. Гольдштейн М.Л., Закурдаев Н.В., Шарф С.В. и др. Локальный интерфейсно-коммуникационный комплекс для МВС // Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр. Вып. 2.]. Екатеринбург, 1998. C. 77-85.


Примечания

... ПОЛЕ ТЯГОТЕНИЯ *
 Работа выполнена при поддержке Российского фонда фундаментальных исследований, гранты N 97-01-00672 и N 99-07-90441.
... случаях1
 Время обсчета одного пакета заданий [1] больше времени связи между мастером и самым далеким рабочим.
... переменных 2
Электронный вариант статьи размещен по адресам:
http://home.ural.ru/~iagsoft/trasbo2_2.html,
http://dcs.imm.uran.ru/~u0100/IAGSoft/trasbo2_2_.html.
... тяготения 3
Электронный вариант статьи размещен по адресам:
http://home.ural.ru/~iagsoft/trasbo2_1.html,
http://dcs.imm.uran.ru/~u0100/IAGSoft/trasbo2_1_.html.





Иванов А.Г. Применение параллельной программы поиска минимума функции многих переменных к задаче о брахистохроне в центральном поле тяготения // Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр.]. Екатеринбург: УрО РАН, 1999, Вып. 3, с.81-94.
PSzipСтатья в формате PostScript (145K)




Home Public ElePub I
Главное меню | Публикации | Электронные публикации | Обо мне |