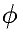 - азимут,
- азимут, 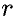 - полярный радиус) с
центром, совпадающим с центром тяготения. Гравитационная постоянная и
массы тел для упрощения выкладок взяты равными единице. Таким образом,
сила, действующая на точку, по абсолютной величине равна
- полярный радиус) с
центром, совпадающим с центром тяготения. Гравитационная постоянная и
массы тел для упрощения выкладок взяты равными единице. Таким образом,
сила, действующая на точку, по абсолютной величине равна
Описывается применение универсальной параллельной программы построения линий уровня звездчатых функций для конкретной задачи -- построение изохрон в нетрадиционной постановке задачи о брахистохроне (движение в центральном поле тяготения). Проводится исследование эффективности распараллеливания. Приведенные результаты вычислений могут быть полезны при преподавании курса вариационного исчисления.
Задача о брахистохроне состоит в отыскании траектории, по которой материальная точка под действием силы тяжести переместилась бы из заданной начальной точки в заданную конечную точку за минимальное время. В отличие от традиционной постановки [1], предполагается, что сила тяжести не является постоянной по величине и направлению. Моделируется закон всемирного тяготения Ньютона -- центральное поле тяготения с силой тяжести, обратно пропорциональной квадрату расстояния до центра тяготения. Начальная скорость точки равна нулю, трение не учитывается. Все тела, включая расположенное в центре тяготения, считаются точечными (не имеют размера).
Специфика поля тяготения подсказывает проводить выкладки в полярной
системе координат (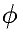 - азимут,
- азимут, 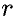 - полярный радиус) с
центром, совпадающим с центром тяготения. Гравитационная постоянная и
массы тел для упрощения выкладок взяты равными единице. Таким образом,
сила, действующая на точку, по абсолютной величине равна
- полярный радиус) с
центром, совпадающим с центром тяготения. Гравитационная постоянная и
массы тел для упрощения выкладок взяты равными единице. Таким образом,
сила, действующая на точку, по абсолютной величине равна
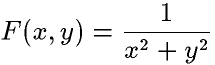 .
.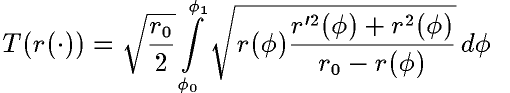 .
.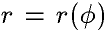 - функция, определяющая траекторию движения точки,
- функция, определяющая траекторию движения точки,
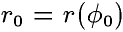 - радиус начальной точки,
- радиус начальной точки,
При нахождении минимума функционала используется метод Эйлера [2] -- приближение искомой кривой кусочно-линейной ломаной. Тем самым задача сводится к нахождению минимума функции многих переменных. Последняя задача решается с помощью измененного метода Хука-Дживса. Этот метод отличается от стандартного метода Хука-Дживса [3] большей степенью перебора.
Для рассматриваемой задачи определенный интерес представляет следующее исследование: как изменяется время спуска по оптимальной траектории при изменении точки окончания процесса (<<нижней>> граничной точки), при этом начальная (<<верхняя>>) точка фиксируется. Достаточной наглядностью обладают иллюстрации в виде линий уровня времени оптимального спуска -- изохроны. Как показали исследования (расчет времени на сетке <<нижних>> граничных точек), функция оптимального времени является звездчатой. В связи с этим было решено использовать программу построения линий уровня звездчатых функций, которая описана в [4]. Для определенности центр тяготения совмещается с началом координат, в качестве исходной (<<верхней>> граничной точки) взята точка с координатами (1, 0).
Рассматриваемый алгоритм создан на основе программы, описанной в [4]. Изменился алгоритм работы задачи-мастера, так как в отличие от транспьютерных систем на использованном многопроцессорном комплексе МВС-100 не поддерживается работа параллельных потоков (конвейеров) на одном процессорном узле. Несущественные изменения внесены также в алгоритм обработки луча.
Алгоритм вычисления линий уровня основан на том, что множества уровня являются звездчатыми множествами, причем центр звездчатости для самого нижнего уровня является центром звездчатости для больших уровней. Таким образом, еcли мы проведем из центра звездчатости луч, то он пересечет каждую линию уровня только один раз, и пересечения будут происходить по возрастанию уровней. Можно заметить, что квазивыпуклые функции удовлетворяют высказанным требованиям.
Если мы выпустим из <<центральной>> точки равномерно по азимуту некоторое количество лучей и найдем точки их пересечения с линиями уровня, то в итоге получим аппроксимацию линий уровня. Нахождение пересечения луча с линией уровня сводится к отысканию корня некоторой функции.
Назовем радиусом линии уровня на соответствующем луче расстояние от центральной точки до точки пересечения линии уровня с данным лучом.
Алгоритм поиска радиусов линий уровня на луче для всех заказанных линий уровня назовем алгоритмом обработки луча. Этот алгоритм последовательно находит точки пересечения лучей с заказанными линиями уровня. Задача нахождения одной такой точки пересечения сводится к решению нелинейного уравнения. Для решения такого уравнения используется модифицированный метод хорд. Каждое вычисление точки пересечения луча с линией уровня требует неоднократного вычисления исследуемой функции.
В естественных случаях при малом угле между лучами радиусы одной линии уровня на близких лучах будут близки. Поэтому при обработке лучей в качестве начального приближения для очередного луча разумно брать радиусы с ближайшего обработанного луча.
Алгоритм рабочего не претерпел принципиальных изменений по сравнению с [4]. Он состоит в приеме сообщения с начальными приближениями для рассчитываемого луча, вычислении уточненных значений радиусов, пересылке результатов счета центральному процессору (мастеру). Этот цикл повторяется до тех пор, пока не будет получен признак окончания работы.
В статье [4] рассматривалась программа построения линий уровня звездчатых функций для вычислительных сетей на базе транспьютеров. В настоящей работе рассматривается вычислительная сеть на базе микропроцессоров, что несколько усложнило алгоритм задачи-мастера. В транспьютерной системе имелась возможность запускать на одном процессоре несколько параллельных конвейеров (threads), что позволяло проводить вычисления на мастере параллельно с приемом и передачей сообщений рабочим. В рассматриваемой системе каждый процессорный элемент представляет собой обыкновенную последовательную машину, что несколько затрудняет организацию обслуживания рабочих параллельно с обработкой лучей.
В связи со сказанным при работе над программой рассматривалось несколько вариантов алгоритма работы задачи-мастера.
При большом числе процессоров задача-мастер не занимается
<<полезными>> вычислениями, она обеспечивает обмен с рабочими и вывод
результатов по окончании всех вычислений. До окончания обработки всех
лучей на мастере повторяется цикл по всем рабочим. В зависимости от
состояния рабочего проводятся конкретные действия по взаимодействию:
- передача очередного задания на счет;
- тестирование окончания передачи задания;
- запуск приема результатов счета;
- тестирование окончания приема результатов;
- запись результатов в массив;
- обновление массива начальных приближений;
- передача признака окончания работы.
Этот алгоритм условно назовем Gамма.
Очевидно, что при малом числе процессоров необходимо часть <<полезных>> вычислений переложить на плечи задачи-мастера.
Неэффективность подхода, изложенного в предыдущем абзаце, особенно наглядна в случае двух процессоров. Один из возможных вариантов в таком случае -- введение в процедуру обработки луча на задаче-мастере периодических обращений к процедуре обмена с рабочими. Но такой подход на первом этапе был отвергнут по соображениям унификации подпрограммы обработки луча на мастере и рабочих. Поэтому остановились на следующем алгоритме: программа-мастер уходит на обработку луча только в том случае, когда не ожидается приема ни от одного рабочего, т.е. для всех рабочих не закончена передача задания на счет. Этот алгоритм назовем Beta. Обобщенная блок-схема приведена на рис. 1. Такой алгоритм оказывается более эффективным, чем Gamma при малом числе процессоров. Однако при хорошей эффективности распараллеливания для двух процессоров эта схема дает худшие результаты для трех и более процессоров.
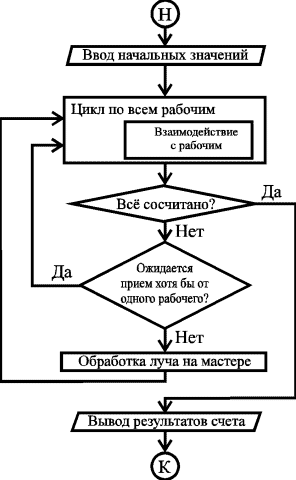 |
| Рис. 1. Алгоритм Beta |
Здесь еще не обсуждался вопрос о том, при каком числе процессоров использовать алгоритм Beta, а при каком Gamma. По результатам численных экспериментов было выработано правило: при числе процессоров, большем трех, используется алгоритм Gamma (корневой процессор не обсчитывает лучи), в противном случае -- алгоритм Beta. Такой комбинированный алгоритм назовем Jota.
Плохая эффективность распараллеливания при малом числе процессоров для Jota стала причиной разработки следующего алгоритма Kappa. В этом алгоритме нет унификации подпрограммы обработки луча на мастере и рабочих. Программа обработки луча для корневого процессора была переработана так, чтобы стало возможным прерывание процесса обработки луча. После вычисления точки пересечения каждой линии уровня с лучом происходит прерывание обработки луча и переход к обмену (цикл по всем рабочим). Сравнение этого метода с методом Jota показало преимущество метода Kappa при сравнительно малом числе процессоров (меньше 11-13).
Был разработан алгоритм Kappa-K, отличающийся от исходного Kappa более частым тактом прерывания обработки луча на мастере. Прерывание обработки луча происходит после каждого вычисления исследуемой функции. Алгоритм Kappa-K показал наилучшие результаты при любом числе процессоров. Все приведенные ниже результаты, если это не указано иначе, получены при использовании этого алгоритма. Обобщенные блок-схемы алгоритмов Kappa и Kappa-K приведены на рис. 2.
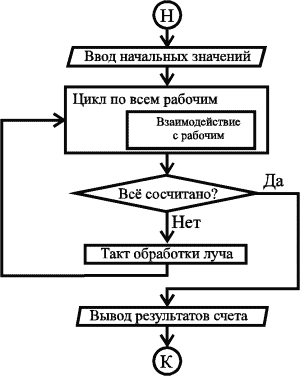 |
| Рис. 2. Алгоритмы Kappa и Kappa-K |
Программа построения линий уровня функций двух переменных со звездчатыми множествами уровня ориентирована на систему МВС-100. Язык программирования -- Portland C. Для расчета линий уровня следует написать на языке Си функцию, вычисляющую функцию двух переменных, и задать в файле необходимые данные для вычисления линий уровня.
Результатом работы программы является файл с координатами точек линий уровня. При использовании библиотеки Grec2 программа формирует векторный графический метафайл с изображением линий уровня. Этот метафайл можно преобразовать в другие графические форматы или посмотреть на персональном компьютере (созданы программы для сред DOS и Windows). Кроме того, создается метафайл с гистограммой загрузки процессоров лучами (для каждого процессора приводится количество обработанных лучей). Если в ходе вычислений программа обнаруживает нарушение звездчатости рассматриваемой функции, будет выдана соответствующая диагностика. Точки, соответствующие лучу, на котором было обнаружено нарушение звездчатости, помечаются на графике маркером.
Приведенные в этом пункте графики построены при помощи графической библиотеки Grec2 -- адаптации библиотеки, описанной в [4].
Универсальная программа построения линий уровня при помощи библиотеки Grec2 формирует рисунок, в правой части которого изображаются собственно графики линий уровня, а в левой части -- проекции графика функции двух переменных на две вертикальные взаимно перпендикулярные плоскости. Проекции изображаются на основе вычисленных линий уровня. Для экономии времени можно сосчитать линии уровня в интересуемом секторе.
На рис. 3 показаны линии уровня оптимального времени (изохроны) для рассматриваемой задачи. Были взяты следующие параметры задачи о брахистохроне: количество звеньев ломаной - 6, точность алгоритма Хука-Дживса - 0.0002. Параметры построения линий уровня: количество лучей - 240, точность по лучу - 3 x 10-4, количество линий уровня - 17, координаты <<центральной>> точки - (0.9, 0.0). На рисунке приведены линии для уровней 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.2.
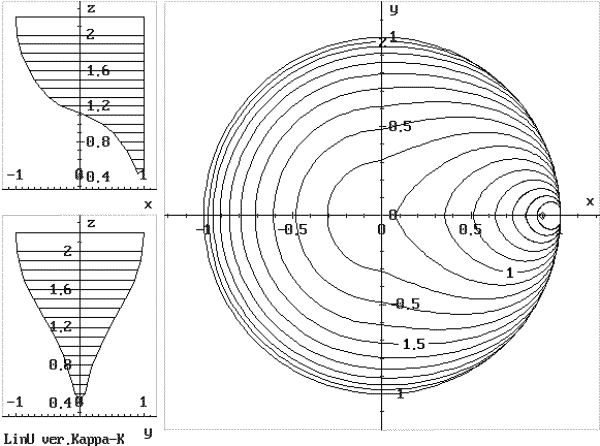 |
| Рис. 3. Изохроны, общий вид |
На рис. 4 подробнее изображена <<центральная>> часть линий уровня -- линии, близкие к началу координат (центру тяготения). Параметры задачи о брахистохроне остались без изменения.
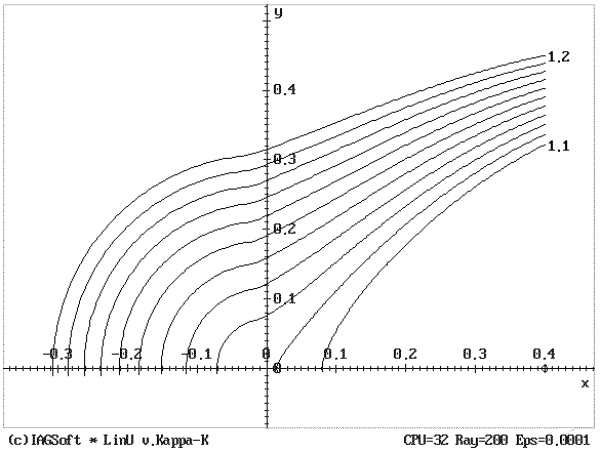 |
| Рис. 4. Изохроны, подробное изображение в окрестности начала координат |
Параметры построения линий уровня для рис. 4: количество лучей - 200, точность по лучу - 1 x 10-4, координаты <<центральной>> точки - (0.4, 0.0). На рисунке приведены линии в сегменте азимутов от 90o до 181o для уровней от 1.1 до 1.2 с шагом 0.01.
При оценке эффективности распараллеливания можно применять
различные показатели. Рассмотрим, например, <<относительное время
выполнения на n процессорах>>, вычисляемое следующим образом:
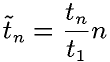 .
.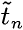 равно единице для
любого числа процессоров.
равно единице для
любого числа процессоров.
В табл. 1 приведены данные времени выполнения для рис. 3. Видно, что в случае большого времени обработки одного луча данный алгоритм позволяет получить хорошую эффективность распараллеливания.
Парадоксальный результат, состоящий в том, что относительное время выполнения оказалось меньшим единицы, можно объяснить следующим образом. Обработка каждого луча не является полностью независимой от других лучей: начальные приближения для радиусов зависят от предыстории выполнения, поэтому в одном случае может <<повезти>> и начальные приближения будут удачными, в другом случае <<не повезет>> и время обработки луча резко возрастет.
При меньшем числе лучей (180) и малом времени обработки луча (число звеньев в методе Эйлера -- 3, точность алгоритма Хука-Дживса -- 0.005, количество линий уровня -- 13) накладные расходы возрастают с увеличением числа процессоров (табл. 2).
| Число процессоров | Время счета, мин | Относительное время 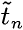 |
| 1* | 432.4 x 4 = 1729.7 | 1 |
| 2* | 212.4 x 4 = 849.5 | .9872122 |
| 3* | 144.1 x 4 = 576.3 | 1.006268 |
| 4* | 109.5 x 4 = 437.8 | 1.0201 |
| 4 | 435.7 | 1.017751 |
| 6 | 294.6 | 1.032234 |
| 8 | 219.0 | 1.023124 |
| 10 | 176.7 | 1.031883 |
| 12 | 147.2 | 1.031533 |
| 14 | 127.7 | 1.04403 |
| 16 | 111.6 | 1.042745 |
| 18 | 100.8 | 1.059564 |
| 20 | 90.21 | 1.053607 |
| 22 | 85.67 | 1.10064 |
| 24 | 77.16 | 1.081428 |
| 26 | 71.20 | 1.081054 |
| 28 | 65.88 | 1.077223 |
| 29 | 63.66 | 1.078099 |
| 30 | 63.20 | 1.107216 |
| 31 | 61.45 | 1.112443 |
| 32 | 59.27 | 1.10759 |
| Число процессоров | Время счета, сек. | Относительное время 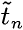 |
| 1 | 643.521 | 1 |
| 2 | 333.975 | 1.037961 |
| 3 | 231.597 | 1.079671 |
| 4 | 173.404 | 1.077845 |
| 5 | 139.989 | 1.08768 |
| 6 | 118.962 | 1.109167 |
| 7 | 102.986 | 1.120246 |
| 8 | 88.8316 | 1.104319 |
| 10 | 72.3083 | 1.123635 |
| 12 | 60.3197 | 1.124806 |
| 14 | 54.0893 | 1.17673 |
| 16 | 48.7099 | 1.211085 |
| 20 | 40.3581 | 1.25429 |
| 24 | 33.1056 | 1.234667 |
| 28 | 29.052 | 1.264071 |
| 29 | 28.1814 | 1.269983 |
| 30 | 28.3492 | 1.321598 |
| 32 | 27.1492 | 1.350033 |
На рис. 5, 6 приведены графики зависимости относительного времени от числа процессоров для алгоритмов Jota, Kappa, Kappa-K. На рис. 5 параметры счета соответствуют табл. 1, на рис. 6 -- табл. 2. Из таблиц видно преимущество алгоритма Kappa-K при любом числе процессоров.
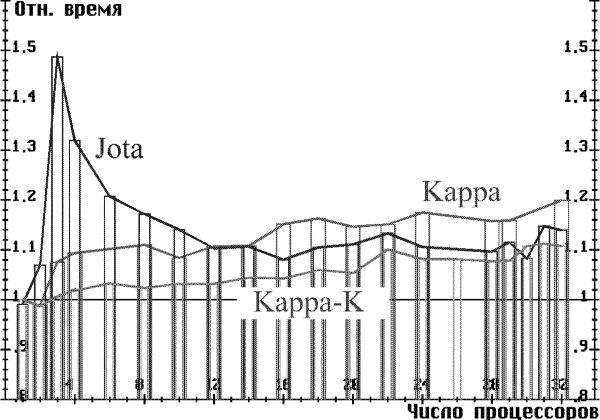 |
| Рис. 5. Относительное время выполнения для разных алгоритмов. Большое время обработки луча |
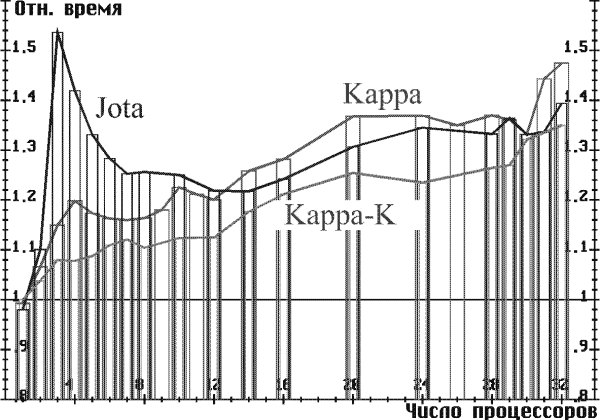 |
| Рис. 6. Относительное время выполнения для разных алгоритмов. Малое время обработки луча |
По результатам работы следует сказать, что применение многопроцессорного вычислительного комплекса МВС-100 позволяет получить результаты, которые на традиционной ВТ не доступны за разумное время. Например, время счета рис. 3 на 16 процессорах составляет менее двух часов, на одном процессоре этот рисунок можно было бы получить за время порядка суток.