Уральское отделение Российской академии наук
Институт математики и механики
Алгоритмы и программные средства параллельных
вычислений — 2000. Вып. 4




РАСЧЕТ КОНСТАНТ СКОРОСТЕЙ
ЭЛЕМЕНТАРНЫХ РЕАКЦИЙ
ПРОЦЕССА ДИНАМИЧЕСКОГО
КИНЕТИЧЕСКОГО РАСЩЕПЛЕНИЯ1

А.Г. Иванов, В.П. Краснов, С.И. Кумков


1. Введение

Процессы динамического кинетического расщепления представляют большой интерес для синтетической органической химии, поскольку позволяют получать оптически чистые соединения, не прибегая к сложным методам разделения. Важные данные о механизме такого рода химических реакций и факторах, определяющих стереоселективность, можно извлечь из результатов изучения кинетики их протекания. Результат реакций существенно зависит от условий (катализатор, температура и т.д.). Для оценки эффективности процесса динамического кинетического расщепления необходимо знание констант скоростей элементарных реакций. Прямое измерение констант скоростей невозможно. Константы можно определять путем решения обратной задачи по имеющимся замерам концентраций реактантов. Значения концентраций известны с некоторой ошибкой, определяемой погрешностью измерений. Высокая стоимость компонентов, участвующих в реакции, не позволяет проводить большое число экспериментов, чтобы применить традиционную статистическую обработку получаемых результатов.

2. Постановка задачи

Реакция динамического кинетического расщепления в случае взаимодействия производных 4-галогенглутаминовой кислоты с ариламинами может быть описана [1] системой дифференциальных и алгебраических уравнений с соответствующими начальными условиями:

    $\displaystyle \dot{A}$(t) = - k3A(t)E(t) - k1A(t)X(t) + k2B(t)X(t),  
    $\displaystyle \dot{B}$(t) = - k4B(t)E(t) + k1A(t)X(t) - k2B(t)X(t),  
    $\displaystyle \dot{C}$(t) = k3A(t)E(t),  
    $\displaystyle \dot{D}$(t) = k4B(t)E(t),  
    X(t) = C(t) + D(t),  
    E(t) = E0 - 2X(t),  
    A(0) = A0,  B(0) = B0,  C(0) = 0,  D(0) = 0.                     (1)

Переменные A, B — концентрации стереоизомеров исходного вещества, C, D — концентрации стереоизомеров продукта реакции, X — концентрация галогенид-иона, E — концентрация катализатора, k1, k2, k3, k4 — константы скоростей элементарных химических реакций. По смыслу задачи все указанные величины неотрицательны.

При подcтановке алгебраических уравнений в дифференциальные получаем систему нелинейных обыкновенных дифференциальных уравнений:

$\displaystyle \dot{A}$ = (k1 - 2k3)A2 + ((2(A0 + B0) - E0)k3 - k1(A0 + B0))A +  
    + (k1 - k2 - 2k3)AB + (A0 + B0)k2B - k2B2,  
$\displaystyle \dot{B}$ = (k2 - 2k4)B2 + ((2(A0 + B0) - E0)k4 - k2(A0 + B0))B +  
    + (k2 - k1 - 2k4)AB + (A0 + B0)k1A - k1A2,  
$\displaystyle \dot{C}$ = 2k3A2 + 2k3AB + (E0 - 2(A0 + B0))k3A,  
$\displaystyle \dot{D}$ = 2k4B2 + 2k4AB + (E0 - 2(A0 + B0))k4B. (2)

Концентрации A0, B0 и E0 известны точно. Во время течения реакции в отдельные моменты ti производятся замеры концентраций A(ti), B(ti), C(ti) и D(ti). Точность замеров описывается относительной и абсолютной погрешностями, так что в каждый момент ti для каждого из веществ A, B, C, D известен интервал (“ворота”), в котором должно находиться истинное значение концентрации:

A(ti) $\displaystyle \in$ [ZminAi, ZmaxAi],   B(ti) $\displaystyle \in$ [ZminBi, ZmaxBi],
C(ti) $\displaystyle \in$ [ZminCi, ZmaxCi],   D(ti) $\displaystyle \in$ [ZminDi, ZmaxDi].

Неизвестными в задаче являются константы k1, k2, k3, k4. Необходимо найти все возможные значения этих параметров, совместимые с “воротами” замеров, т. е. такие, которые обеспечивали бы при численном моделировании системы (2) прохождение смоделированных концентраций через все ворота замеров. Соответствующее множество назовем множеством совместных коэффициентов (“set membership uncertainty” [2]) или, по-другому, информационным множеством.

3. Решение задачи

Система (2) является системой дифференциальных уравнений с элементами жесткости [3,4].

Для численного решения системы (2) разработана эмпирическая численнная процедура с автоматическим переключением между методами интегрирования и автоматическим выбором шага интегрирования. При определенных значениях фазовых переменных интегрирование ведется методом Рунге-Кутта четвертого порядка, при других значениях — первые два уравнения системы (1) подменяются алгебраическими соотношениями

A = 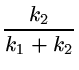$\displaystyle {\frac{k_2}{k_1 + k_2}}$(A0 + B0 - C - D),
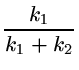B = $\displaystyle {\frac{k_1}{k_1 + k_2}}$(A0 + B0 - C - D),

а остальные уравнения интегрируются методом Эйлера. Обоснование такой подмены содержится в [4].

Для удобства задачу поиска информационного множества разбили на две подзадачи:

I — Нахождение хотя бы одной четверки констант k1, k2, k3, k4, которая соответствовала бы всем воротам замеров (нахождение одной точки информационного множества).

II — Нахождение множества всех четверок констант k1, k2, k3, k4, удовлетворяющих всем воротам замеров (нахождение информационного множества).

3.1 Подзадача I

Для нахождения хотя бы одной четверки констант была использована разработанная ранее параллельная программа поиска минимума скалярной функции многих переменных [5]. Сконструирована вспомогательная подпрограмма, которая получает в качестве параметров значения констант k1, k2, k3, k4, проводит численное моделирование химической реакции, выдает в качестве значения невязку между концентрациями при моделировании и воротами замеров. Невязка должна обладать следующим свойством: если хотя бы одно значение смоделированной концентрации проходит мимо ворот хотя бы одного замера, то невязка положительна, если же все смоделированные концентрации проходят через ворота, то значение невязки неположительно.

Сконструировано несколько различных вариантов подпрограммы невязки. В одном из них минимизируется максимальное расстояние рассчитаных концентраций от границ ворот замеров (если рассчитанная концентрация оказывается внутри ворот, то расстояние считается отрицательным):

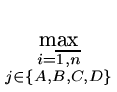
f1($\displaystyle \;\stackrel{\to}{K}\;$) = $\displaystyle \max\limits_{{\scriptstyle i = \overline{1,n}} \atop \scriptstyle j \in \{A,B,C,D\} }^{}$$\displaystyle \left(\vphantom{\, \max \left\{\, z^j_i(\stackrel{\to}{K})-Zmax^j_i,\ Zmin^j_i - z^j_i(\stackrel{\to}{K}) \right\} }\right.$ max$\displaystyle \left\{\vphantom{\, z^j_i(\stackrel{\to}{K})-Zmax^j_i,\ Zmin^j_i - z^j_i(\stackrel{\to}{K}) }\right.$ zji($\displaystyle \;\stackrel{\to}{K}\;$) - Zmaxji,I>Zminji - zji($\displaystyle \;\stackrel{\to}{K}\;$)$\displaystyle \left.\vphantom{\, z^j_i(\stackrel{\to}{K})-Zmax^j_i,\ Zmin^j_i - z^j_i(\stackrel{\to}{K}) }\right\}$$\displaystyle \left.\vphantom{\, \max \left\{\, z^j_i(\stackrel{\to}{K})-Zmax^j_i,\ Zmin^j_i - z^j_i(\stackrel{\to}{K}) \right\} }\right)$,

где $ \;\stackrel{\to}{K}\;$ = (k1, k2, k3, k4)' $ \in$ IR4 — вектор коэффициентов, zji($ \;\stackrel{\to}{K}\;$) — прогноз (рассчитанная концентрация вещества j в момент ti).

Другой вариант для невязки можно записать следующим образом:

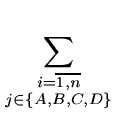f2($\displaystyle \;\stackrel{\to}{K}\;$) = $\displaystyle \sum_{{\scriptstyle i = \overline{1,n}} \atop \scriptstyle j \in \{A,B,C,D\} }^{}$g2(zji($\displaystyle \;\stackrel{\to}{K}\;$), Zminji, Zmaxji),

где

g2(z, Zmin, Zmax) = $\displaystyle \left\{\vphantom{ \begin{array}{ll} (Zmin - z)^2 \ , & z < Zmin \... ...z \leq Zmax \ , \\ [0.5ex] (z - Zmax)^2 \ , & z > Zmax \ . \end{array}}\right.$$\displaystyle \begin{array}{ll} (Zmin - z)^2 \ , & z < Zmin \ , \\ [0.5ex] 0 \... ...in \leq z \leq Zmax \ , \\ [0.5ex] (z - Zmax)^2 \ , & z > Zmax \ . \end{array}$

При решении подзадачи I последовательно перебираются все имеющиеся функции невязки. Поэтому существует большая вероятность, что хотя бы в одном из этих случаев будет найден именно глобальный минимум. Отметим также, что успешным решением подзадачи I является нахождение хотя бы одной четверки $ \;\stackrel{\to}{K}\;$, для которой значение функции невязки отрицательно. Такое значение может получаться (и это нас устраивает) и на локальном минимуме.

Так как размерность аргумента минимизируемой функции невелика — равна четырем (в случае неопределенности по начальным условиям — пяти), то оптимальное число процессоров, используемых в вычислениях, составило 8 ™ 16 (вычислитель МВС-100 [6]).

Результатом решения подзадачи I являются значения величин k1, k2, k3, k4 наилучшие с точки зрения прохождения смоделированных концентраций через ворота, что соответствует наилучшему (в некотором смысле) приближению к реальным константам k1, k2, k3, k4.

Если же минимальное значение невязки оказывается положительным, это означает, что либо были взяты слишком узкие ворота (завышена точность измерительных приборов), либо в ансамбле замеров один или несколько замеров оказались “глупыми”.

3.2 Подзадача II

Для нахождения всех четверок k1, k2, k3, k4, удовлетворяющих замерам (информационного множества), используется перебор по четырехмерной сетке. В качестве начальной используется сетка, построенная вокруг точки, которая является решением подзадачи I. В дальнейшем сетка корректируется по результатам счета, исходя из предположения односвязности информационного множества.

Четырехмерная сетка организована как произведение двух сеток — сетки по k1 и k2 (сетка 12) и сетки по k3 и k4 (сетка 34). Сетка 34 — прямоугольная, сетка 12 в зависимости от потребности может быть задана прямоугольной, косоугольной (параллелограммной) или секториальной с переменным шагом по радиусу.

Распараллеливание ведется по схеме процессорной фермы. Один процессор назначается процессором вывода, все остальные — рабочими. Минимальным заданием для рабочего является расчет сетки 34 при фиксированном узле сетки 12.

Под расчетом сетки подразумевается заполнение массива флагов, в котором каждый элемент соответствует узлу сетки 34. Паре узлов сетки 12 и сетки 34 соответствует конкретная четверка констант k1, 2, 3, 4. Если при численном моделировании протекания реакции (с использованием этих констант k1, 2, 3, 4) концентрации выйдут за рамки хотя бы одних ворот, то соответствующий флаг устанавливается в положение “вне множества”. Если концентрации проходят через все ворота, то флаг устанавливается в положение “внутри множества” — соответствующий узел сетки лежит внутри информационного множества. В программе массив флагов реализован как массив char[].

Распределение заданий между рабочими процессорами является статическим — каждый процессор заранее знает задания (номера узлов сетки 12), которые ему необходимо рассчитать. Такой способ распределения заданий теоретически не является оптимальным, но позволяет сократить число обменов между рабочими процессорами и процессором вывода, что при большом размере процессорной сети и особенностях2 системы МВС-100 может существенно снизить накладные расходы.

Если после расчета задания все флаги в массиве флагов оказываются в положении “вне множества”, то рабочий переходит к вычислению следующего задания (передачи информации на процессор вывода не происходит). Если хотя бы один флаг оказывается в положении “внутри множества”, то рабочий передает на процессор вывода массив флагов и соответствующий номер узла сетки 12. Таким образом, передача информации осуществляется только в том случае, если узел сетки 12 лежит внутри информационного множества. Такой алгоритм дополнительно сокращает трафик процессорной сети. Передача массива флагов осуществляется путем передачи всего массива char[], где каждому флагу соответствует один байт. В дальнейшем для экономии времени передачи возможно организовать кодирование “восемь флагов в одном байте” (или даже run-length кодирование).

После вычисления всех своих заданий рабочий посылает процессору вывода сообщение “рассчитал все задания”. Необходимость в этом сообщении имеется не всегда. Если последнее задание рабочего оказалось не пустым (информационное множество для соответствующей сетки 34 непусто), то процессор вывода сам может понять, что этот рабочий выполнил все вычисления, но в настоящей версии программы такое сообщение посылается в любом случае.

Процессор вывода поддерживает два массива флагов — для сетки 12 и для сетки 34 (реализованы как массивы int[]). Начальное значение флагов сетки 12 – “узел не рассчитан”, начальное значение флагов сетки 34 – “число узлов = 0”. После получения массива флагов от рабочего процессор вывода выполняет следующие действия:
1) “прибавляет” полученный массив к собственному массиву сетки 34 (если соответствующий флаг в полученном массиве имеет значение “внутри множества”, то значение флага “число узлов = n” заменяется на “число узлов = n + 1”),
2) устанавливает в “число узлов = k” соответствующий элемент массива флагов сетки 12, где k – число флагов с признаком “внутри множества” в полученном массиве,
3) меняет (если необходимо) с “узел не рассчитан” на “пустой узел” флаги, соответствующие узлам сетки 12, которые рабочий просчитал, но не передал результаты процессору вывода.

В конце работы на процессоре вывода имеем два заполненых массива флагов для сетки 12 и сетки 34, которые отображают проекции информационного множества на плоскости k1k2 и k3k4. Эти проекции сбрасываются на диск в графическом и числовом виде. Для создания графики используется библиотека GREC3.

Максимальные размеры сетки в настоящей версии программы, обусловленные типом использованных переменных и массивов: сетка 12 – не более 32767 точек, сетка по k3 – не более 127 точек, сетка по k4 – не более 127 точек.

Рассмотренный алгоритм позволяет получить частичные результаты при заказе в паспорте задания меньшего, чем требуется, времени счета. Процессор вывода при подходе времени к окончанию сбрасывает результаты, особо помечая неподсчитанные узлы сетки 12.

Поскольку программа изначально была рассчитана на многопроцессорную работу (запустить программу на одном процессоре невозможно), оценить эффективность распараллеливания можно только косвенно.


Количество Время счета Время счета
процессоров “брутто”, мин. процессора вывода, сек.
5 33 (165) 1938 (9690)
10 16 (160) 877 (8765)
16 10 (160) 555 (8874)
24 8 (192) 400 (9600)
32 7 (224) 306 (7340)
48 5 (240) 211 (10110)
64 5 (320) 165 (10589)

Результаты запуска одной и той же задачи на разном количестве процессоров показаны в таблице. Сообщаемое операционной системой время от начала загрузки процессорной сети до полного окончания счета на всех процессорах — время “брутто”. “Время счета процессора вывода” — время от первого до последнего оператора процессора вывода. В скобках приведено время счета, умноженное на количество процессоров. Эта величина является сравнительным показателем эффективности распараллеливания.

При анализе таблицы следует учесть, что приведенные данные соответствуют нетипичной (маленькой) задаче. Для типичных задач с большим размером сетки (порядка 120×50×100×100 узлов) удалось получить хорошую эффективность расспараллеливания при использовании до 125 процессоров (максимальное количество процессоров МВС-100, имеющееся в ИММ).


4. Результаты вычислений

Рис. 1. Пример решения подзадачи I

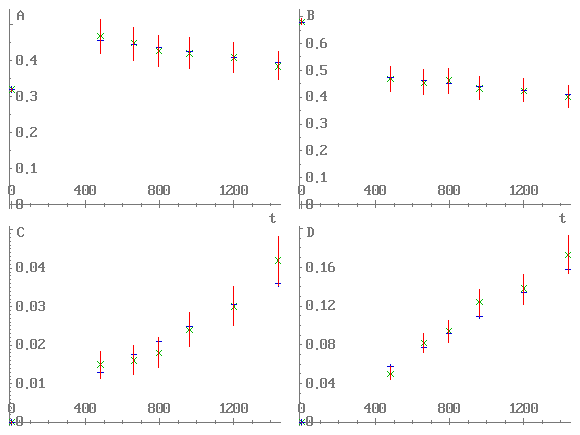На рис. 1 графически изображено решение подзадачи I. Горизонтальная ось — время в минутах, вертикальная ось — относительная концентрация соответствующего вещества. Косыми крестиками (×) обозначены замеры концентраций, вертикальные отрезки — ворота, прямые крестики (+) — смоделированные концентрации, соответствующие решению подзадачи I (т.е. наилучшим константам k1, 2, 3, 4).


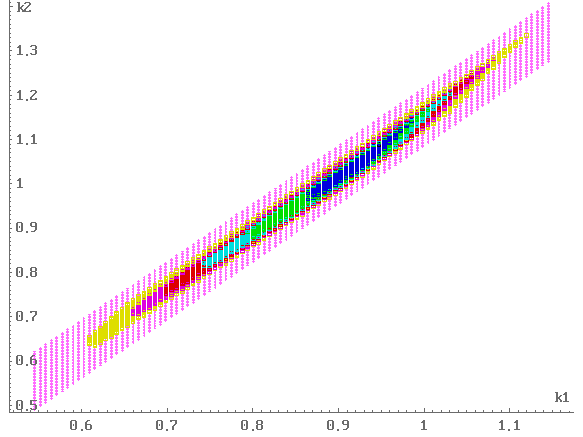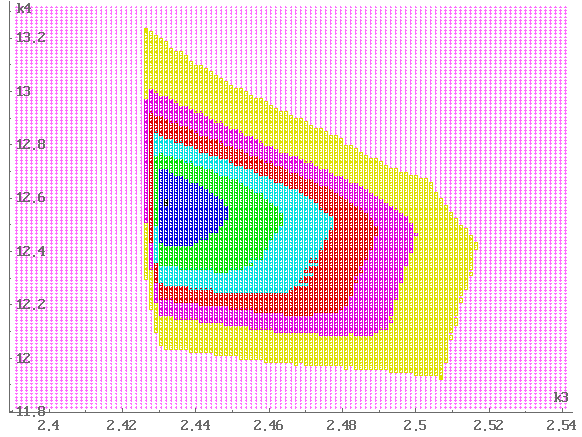
Рис. 2. Проекция информационного множества на плоскость k1k2

На рис. 2, 3 приведены результаты решения подзадачи II. Маленькими крестиками показаны проекции пустых узлов сетки (соответствующее значение флага сетки: “число узлов = 0”), жирными квадратами — проекции, которым соответствует хотя бы один непустой узел.
Рис. 3. Проекция информационного множества на плоскость k3k4

СПИСОК ЛИТЕРАТУРЫ

  1. Краснов В.П., Королева М.А. Нуклеофильное замещение галогена в 4-галогенпроизводных глутаминовой кислоты. Сообщение 1. Влияние растворителя // Изв. АН, Сер. хим., 1995, N 4. С. 652—655.
  2. Milanese M., Norton J. (editors). Bounding Approaches to System Identification. London: Plenum Press, 1996.
  3. Новиков Е.А. Явные методы для жестких систем. Новосибирск: Наука, 1997. 200 с.
  4. Ракитский Ю.В., Устинов С.М., Черноруцкий И.Г. Численные методы решения жестких систем. М.: Наука, 1979. 208 с.
  5. Иванов А.Г. Параллельный алгоритм прямого поиска минимума функции многих переменных4// Алгоритмы и программные средства параллельных вычислений: Вып. 2. Екатеринбург, 1998. С. 110—122.
  6. Игумнов А. С., Коновалов А. В., Самофалов В. В., Шарф С. В. Развитие и адаптация системного программного обеспечения МВС-100 // Алгоритмы и программные средства параллельных вычислений: Вып. 2. Екатеринбург, 1998. С. 123—133.



Обложка книги
Иванов А.Г., Краснов В.П., Кумков С.И. Расчет констант скоростей элементарных реакций процесса динамического кинетического расщепления // Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр.]. Екатеринбург: УрО РАН, 2000, Вып. 4, с.99-110.

PSziptrasbo00.zip — печатная версия в формате PostScript


Home Public ElePub I New! МВС
Главное меню | Публикации | Электронные публикации | Обо мне | Новости | Параллельное программирование

















... РАСЩЕПЛЕНИЯ1
Работа выполнена при поддержке РФФИ, гранты  00-01-00348,  00-03-32776,  99-07-90441,  00-15-97390. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... особенностях2
Сравнительно большие затраты времени на организацию однократного обмена. Время передачи одного байта и килобайта практически не отличается. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... GREC3
http://home.imm.uran.ru/iagsoft/GREC/index_.html 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... переменных 4
 Электронный вариант статьи размещен по адресам:
   http://home.imm.uran.ru/iagsoft/trasbo2_2_.html,
   http://home.ural.ru/~iagsoft/trasbo2_2.html. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
©IAGSoft