Иванов А.Г.
Описывается преподавание классических задач вариационного исчисления с
применением вычислительной техники. Решение задач доводится до построения
функций, удовлетворяющих конкретным граничным условиям.
Рассматриваются разрывные решения.
Аэродинамическая задача Ньютона
 Состоит в отыскании образующей тела вращения с наименьшим сопротивлением в
потоке разреженного идеального газа. Разреженный газ представляется в виде
бесконечно малых частиц, не сталкивающихся друг с другом и зеркально отражающихся
от поверхности тела при столкновении с ним.
Состоит в отыскании образующей тела вращения с наименьшим сопротивлением в
потоке разреженного идеального газа. Разреженный газ представляется в виде
бесконечно малых частиц, не сталкивающихся друг с другом и зеркально отражающихся
от поверхности тела при столкновении с ним.
 Прежде всего задача решается, согласно /1/, в предположении малости
величины (т.е. ).
Соответствующее решение уравнения Эйлера имеет вид
(коэффициент сопротивления ). Для определенности взяты граничные условия
и . Ясно, что допущение о малости величины
является грубым.
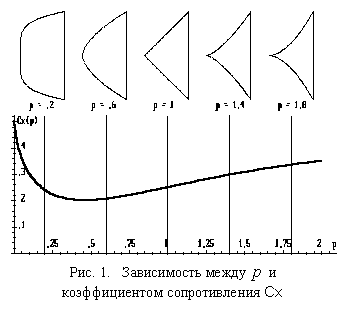
После этого демонстрируется поиск решения в классе функций .
Каждому значению показателя ставится свое значение коэффициента
сопротивления (рис. 1).
Минимальное значение достигается при
().
Прежде всего задача решается, согласно /1/, в предположении малости
величины (т.е. ).
Соответствующее решение уравнения Эйлера имеет вид
(коэффициент сопротивления ). Для определенности взяты граничные условия
и . Ясно, что допущение о малости величины
является грубым.
После этого демонстрируется поиск решения в классе функций .
Каждому значению показателя ставится свое значение коэффициента
сопротивления (рис. 1).
Минимальное значение достигается при
().
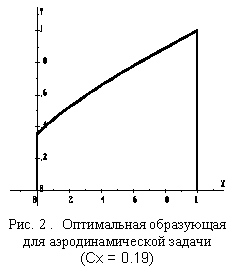
Далее, в рамках численного подхода, демонстрируется программа поиска решения
методом Эйлера (аппроксимация решения кусочно-линейной функцией). При этом задача
сводится к отысканию минимума функции многих переменных. Оптимальное решение
(рис. 2) имеет угловую точку /2/.
Задача о наименьшей поверхности вращения
 Необходимо отыскать образующую поверхности вращения, которая минимизировала бы
площадь этой поверхности. Известно, что искомая образующая -- цепная линия
(гиперболический косинус). В зависимости от конкретных граничных условий могут
существовать два решения уравнения Эйлера (каждое ≈- цепная линия), одно или ни
одного.
Необходимо отыскать образующую поверхности вращения, которая минимизировала бы
площадь этой поверхности. Известно, что искомая образующая -- цепная линия
(гиперболический косинус). В зависимости от конкретных граничных условий могут
существовать два решения уравнения Эйлера (каждое ≈- цепная линия), одно или ни
одного.
 При традиционном изложении, как правило, останавливаются на задаче выбора
оптимальной из двух кривых и не уделяют внимания случаю отсутствия классического
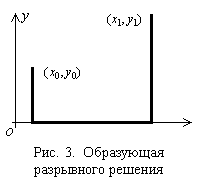
решения. При численном решении методом Эйлера легко обнаруживается разрывное
решение: два диска, образующей для которых служит ломаная, состоящая из двух
вертикальных отрезков и одного горизонтального, лежащего на оси
(Рис. 3). В /3/ доказано,
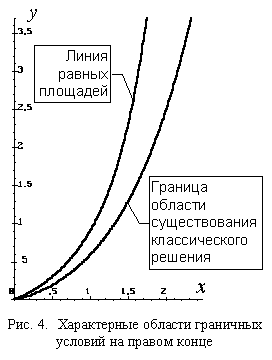
что разрывное решение всегда является локальным минимумом. Более того, даже в
области существования решения уравнения Эйлера можно численно найти подобласть,
где глобальный минимум достигается на разрывном решении. На рис. 4 эта подобласть
расположена между "Линией равных площадей" и
"Границей области
существования классического решения"
(граничные условия на левом конце фиксированы: ,
).
При традиционном изложении, как правило, останавливаются на задаче выбора
оптимальной из двух кривых и не уделяют внимания случаю отсутствия классического
решения. При численном решении методом Эйлера легко обнаруживается разрывное
решение: два диска, образующей для которых служит ломаная, состоящая из двух
вертикальных отрезков и одного горизонтального, лежащего на оси
(Рис. 3). В /3/ доказано,
что разрывное решение всегда является локальным минимумом. Более того, даже в
области существования решения уравнения Эйлера можно численно найти подобласть,
где глобальный минимум достигается на разрывном решении. На рис. 4 эта подобласть
расположена между "Линией равных площадей" и
"Границей области
существования классического решения"
(граничные условия на левом конце фиксированы: ,
).
Задача о брахистохроне
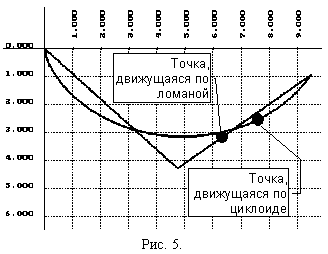 В задаче необходимо найти линию наискорейшего спуска между двумя точками в
вертикальной плоскости. Этой линией является дуга циклоиды. Проблема нахождения
конкретной циклоиды для конкретных граничных условий обычно остается за рамками
изложения. Предлагается демонстрационно-обучающая программа, которая для любых
допустимых граничных условий находит и графически изображает оптимальное решение
в виде циклоиды и оптимальное решение в классе двузвенных ломаных (Рис. 5).
В задаче необходимо найти линию наискорейшего спуска между двумя точками в
вертикальной плоскости. Этой линией является дуга циклоиды. Проблема нахождения
конкретной циклоиды для конкретных граничных условий обычно остается за рамками
изложения. Предлагается демонстрационно-обучающая программа, которая для любых
допустимых граничных условий находит и графически изображает оптимальное решение
в виде циклоиды и оптимальное решение в классе двузвенных ломаных (Рис. 5).
Литература:
1. М.А.Краснов, Г.И.Макаренко, А.И.Киселев.
Вариационное исчисление. М., "Наука", 1973. 2. И.Ньютонъ.
Математическiя Начала Натуральной
Философiи. П., 1916. 3. Н.И.Ахиезер. Лекции по вариационному
исчислению. М., Гостехиздат, 1955. 4. Б.Банди. Методы
оптимизации. М., "Радио и связь", 1988.
© Иванов А.Г.
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru
 Состоит в отыскании образующей тела вращения с наименьшим сопротивлением в
потоке разреженного идеального газа. Разреженный газ представляется в виде
бесконечно малых частиц, не сталкивающихся друг с другом и зеркально отражающихся
от поверхности тела при столкновении с ним.
Состоит в отыскании образующей тела вращения с наименьшим сопротивлением в
потоке разреженного идеального газа. Разреженный газ представляется в виде
бесконечно малых частиц, не сталкивающихся друг с другом и зеркально отражающихся
от поверхности тела при столкновении с ним. Прежде всего задача решается, согласно /1/, в предположении малости
величины (т.е. ).
Соответствующее решение уравнения Эйлера имеет вид
(коэффициент сопротивления ). Для определенности взяты граничные условия
и . Ясно, что допущение о малости величины
является грубым.
После этого демонстрируется поиск решения в классе функций .
Каждому значению показателя ставится свое значение коэффициента
сопротивления (рис. 1).
Минимальное значение достигается при
().
Прежде всего задача решается, согласно /1/, в предположении малости
величины (т.е. ).
Соответствующее решение уравнения Эйлера имеет вид
(коэффициент сопротивления ). Для определенности взяты граничные условия
и . Ясно, что допущение о малости величины
является грубым.
После этого демонстрируется поиск решения в классе функций .
Каждому значению показателя ставится свое значение коэффициента
сопротивления (рис. 1).
Минимальное значение достигается при
().
 Необходимо отыскать образующую поверхности вращения, которая минимизировала бы
площадь этой поверхности. Известно, что искомая образующая -- цепная линия
(гиперболический косинус). В зависимости от конкретных граничных условий могут
существовать два решения уравнения Эйлера (каждое ≈- цепная линия), одно или ни
одного.
Необходимо отыскать образующую поверхности вращения, которая минимизировала бы
площадь этой поверхности. Известно, что искомая образующая -- цепная линия
(гиперболический косинус). В зависимости от конкретных граничных условий могут
существовать два решения уравнения Эйлера (каждое ≈- цепная линия), одно или ни
одного.
 При традиционном изложении, как правило, останавливаются на задаче выбора
оптимальной из двух кривых и не уделяют внимания случаю отсутствия классического
решения. При численном решении методом Эйлера легко обнаруживается разрывное
решение: два диска, образующей для которых служит ломаная, состоящая из двух
вертикальных отрезков и одного горизонтального, лежащего на оси
(Рис. 3). В /3/ доказано,
что разрывное решение всегда является локальным минимумом. Более того, даже в
области существования решения уравнения Эйлера можно численно найти подобласть,
где глобальный минимум достигается на разрывном решении. На рис. 4 эта подобласть
расположена между "Линией равных площадей" и
"Границей области
существования классического решения"
(граничные условия на левом конце фиксированы: ,
).
При традиционном изложении, как правило, останавливаются на задаче выбора
оптимальной из двух кривых и не уделяют внимания случаю отсутствия классического
решения. При численном решении методом Эйлера легко обнаруживается разрывное
решение: два диска, образующей для которых служит ломаная, состоящая из двух
вертикальных отрезков и одного горизонтального, лежащего на оси
(Рис. 3). В /3/ доказано,
что разрывное решение всегда является локальным минимумом. Более того, даже в
области существования решения уравнения Эйлера можно численно найти подобласть,
где глобальный минимум достигается на разрывном решении. На рис. 4 эта подобласть
расположена между "Линией равных площадей" и
"Границей области
существования классического решения"
(граничные условия на левом конце фиксированы: ,
). В задаче необходимо найти линию наискорейшего спуска между двумя точками в
вертикальной плоскости. Этой линией является дуга циклоиды. Проблема нахождения
конкретной циклоиды для конкретных граничных условий обычно остается за рамками
изложения. Предлагается демонстрационно-обучающая программа, которая для любых
допустимых граничных условий находит и графически изображает оптимальное решение
в виде циклоиды и оптимальное решение в классе двузвенных ломаных (Рис. 5).
В задаче необходимо найти линию наискорейшего спуска между двумя точками в
вертикальной плоскости. Этой линией является дуга циклоиды. Проблема нахождения
конкретной циклоиды для конкретных граничных условий обычно остается за рамками
изложения. Предлагается демонстрационно-обучающая программа, которая для любых
допустимых граничных условий находит и графически изображает оптимальное решение
в виде циклоиды и оптимальное решение в классе двузвенных ломаных (Рис. 5). iagsoft@imm.uran.ru
iagsoft@imm.uran.ru