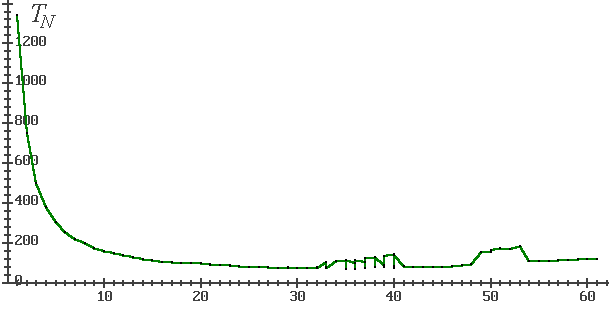
Рис. 1: График в линейных координатах
Параллельная программа безусловной минимизации В приложениях часто встречается задача поиска минимума скалярной функции многих переменных. Во многих случаях исследуемая функция не может быть представлена аналитически - значение функции является результатом работы некоторой численной процедуры. В таких случаях требуется программа, использующая один из методов прямого поиска - метод, не требующий вычисления производных функции.
Автором создана параллельная программа поиска минимума функции многих переменных для многопроцессорного компьютера с разделенной памятью. Разработано три варианта параллельного алгоритма, различающиеся степенью перебора. Алгоритмы созданы на основе известного метода Хука-Дживса.
Показатель эффективности распараллеливания При анализе эффективности распараллеливания часто применяются графики вида (число процессоров) -> (время счета). Такие графики (рис. 1) дают наглядную картину зависимости времени счета от числа процессоров, но не дают возможность легко оценить эффективность распараллеливания. В случае, когда для вывода такого графика используются логарифмические координаты по обеим осям, при абсолютном распараллеливании график зависимости должен быть прямой линией. Но, к сожалению, не всякая прямая соответствует абсолютному распараллеливанию.
 |
Рис. 1: График в линейных координатах |
Предлагается ввести показатель - относительное время выполнения:
|
В графиках можно использовать как саму величину T*N (рис. 2), так и ее логарифм, который можно назвать степень неэффективности распараллеливания. В случае идеального распараллеливания последний показатель равен нулю.
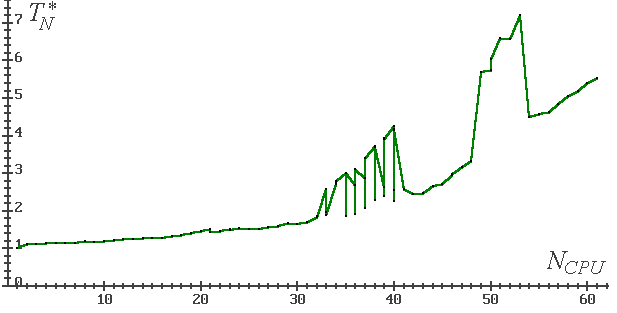 |
Рис. 2: Относительное время счета |
1 Работа поддержана РФФИ. Гранты 97-01-00672,
97-01-00458.
 iagsoft@imm.ural.ru
iagsoft@imm.ural.ru