ПАРАЛЛЕЛЬНАЯ ПРОГРАММА БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ.
ПРИМЕНЕНИЕ В ЗАДАЧЕ ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ХИМИЧЕСКОЙ РЕАКЦИИ

А.Г.Иванов¹, С.И.Кумков¹, В.П.Краснов²

¹ Институт математики и механики УрО РАН, Екатеринбург
² Институт органического синтеза УрО РАН, Екатеринбург

iagsoft@imm.uran.ru

Большое число задач, имеющих важное практическое и теоретическое значение, могут быть сведены к задаче минимизации скалярной функции нескольких переменных:

Использование различного рода градиентных методов не всегда возможно из-за сложной структуры функции f(x₁, x₂,..., x_n). Во многих практических задачах значение функции является результатом вычислений некоторой численной процедуры. Не всегда функция является гладкой или даже непрерывной. Поэтому имеет смысл использовать методы прямого поиска (методы, в которых используются только значения функции).

Рассматриваемый алгоритм создан на основе метода прямого поиска, описанного в [1] как метод Хука-Дживса. Общая идеология этого метода состоит в чередовании поиска вокруг базовой точки, при котором определяется направление убывания функции, и поиска по образцу, при котором происходит корректируемое движение по направлению убывания.

В оригинальном методе Хука-Дживса, как при поиске вокруг базовой точки, так и при поиске вокруг образца, применен существенно последовательный алгоритм - координаты текущей точки для вычисления зависят от значения функции в предыдущей точке. Это не позволяет провести распараллеливание. Кроме того, алгоритм имеет некоторую анизотропию - предпочтительным является направление возрастания аргумента функции. При распараллеливании были разработаны три варианта алгоритма поиска минимума функции многих переменных. Эти алгоритмы различаются глубиной перебора.

Первый алгоритм наиболее близок, по степени перебора, к оригинальному методу Хука-Дживса. Число исследуемых точек в этом алгоритме при однократном поиске вокруг базовой точки равно 2n (n - число аргументов функции). (В оригинальном алгоритме число исследуемых точек зависит от значений функции и лежит в интервале [n, 2n]) В этом алгоритме распараллеливается как поиск по базовой точке, так и поиск по образцу.

Второй и третий алгоритмы отличаются гораздо большей степенью перебора. Для второго алгоритма число точек при поиске вокруг базовой точки равно 2ⁿ, для третьего алгоритма - 3ⁿ-1. В этих алгоритмах используется исходный поиск вокруг образца, который не распараллеливается. Применение этих переборных алгоритмов повышает вероятность нахождения глобального минимума.

Распараллеливание ведется по схеме процессорной фермы. Задача-мастер реализует алгоритм поиска минимума функции, обращаясь, по необходимости, к задачам-рабочим для вычисления значений минимизируемой функции. Рабочий принимает задание от мастера, вычисляет значения функции в точках задания, находит их минимум и отправляет результат мастеру.

Для увеличения эффективности поиска в программу введены элементы метода Монте-Карло - в моменты возможного простоя задача-мастер вычисляет значения функции в случайных точках, в дальнейшем эти значения используются в оптимизационном процессе наравне с "предопределенными" точками [2].

Параллельная программа написана на языке Си для операционной системы Router. Программа отлаживалась и работала на вычислительных системах МВС-100/1000.

Параллельная программа использовалась в задаче идентификации параметров химической реакции.

Реакция динамического кинетического расщепления может быть описана системой дифференциальных уравнений:

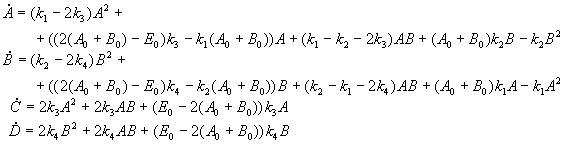   (2)

A, B - концентрации стереоизомеров исходного вещества, C, D - концентрации стереоизомеров продукта реакции, E₀ - начальная концентрация катализатора, k₁, k₂, k₃, k₄ - константы скоростей элементарных химических реакций. По смыслу задачи все указанные величины неотрицательны.

Концентрации A₀, B₀ и E₀ известны точно. Во время течения реакции в отдельные моменты t_i производятся замеры концентраций A_i, B_i, C_i и D_i. Точность замеров описывается относительной и абсолютной погрешностями, так что в каждый момент t_i для каждого из веществ A, B, C, D известен интервал ("ворота"), в котором должно находиться истинное значение концентрации:

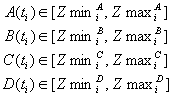             (3)

Неизвестными в задаче являются константы k₁, k₂, k₃, k₄. Необходимо найти все возможные значения этих параметров, совместимые с "воротами" замеров (3), т.е. такие, которые обеспечивали бы при численном моделировании системы (2) прохождение смоделированных концентраций через все ворота замеров. Соответствующее множество можно назвать множеством совместных коэффициентов или, по-другому, информационным множеством.

Первым этапом нахождения информационного множества является нахождение хотя бы одной точки множества, или, другими словами, хотя бы одной четверки k₁, k₂, k₃, k₄, совместной со всеми замерами. Для решения этой задачи применяется рассматриваемая программа минимизации.

Было решено сконструировать функции невязки. Аргументами функций являются константы k₁, k₂, k₃, k₄. Имея константы, функция численно интегрирует систему дифференциальных уравнений (2), а затем сравнивает полученные промоделированные значения с воротами замеров. Если все промоделированные значения (прогнозы) попадают в ворота, то функция невязки выставляет отрицательное значение, если хотя бы один прогноз не попадает в ворота, то функция выставляет положительное значение. Таким образом, если мы будем минимизировать функцию невязки и получим отрицательное значение, то аргумент, при котором достигнут минимум, будет четверкой констант, принадлежащей информационному множеству. Если же минимум окажется положительным, то это еще не значит, что информационное множество пусто, возможно, алгоритм поиска минимума "свалился" в локальный минимум, в этом случае можно попытаться запустить алгоритм из другой начальной точки или применить другую функцию невязки.

Было сконструировано несколько функций невязки. В частности, одна из функций характеризует максимальное расстояние от границ допусков:

где z_i^j - значение, полученное в результате моделирования.

Сконструировано еще несколько функций невязки - с негладкой или разрывной зависимостью от промоделированных значений.

С исследовательскими целями создана функция невязки, представляющую сумму квадратов отклонений прогнозов от замеров. Оказалось, что в большом числе случаев минимизация по критерию квадратичного отклонения дает результат, не совместный с воротами замеров.

После того, как найдена одна точка информационного множества, вокруг нее выстраивается четырехмерная сетка по k₁, k₂, k₃, k₄. Обсчет узлов сетки и формирование информационного множества производятся при помощи специально сконструированной параллельной программы.

Асимметрические синтезы на основе процессов динамического кинетического расщепления представляют большой интерес, поскольку позволяют получить продукты, обогащенные одним стереоизомером из рацемического субстрата или смеси диастереомеров. Важные данные о механизме таких реакций и факторах, определяющих стереоселективность, можно извлечь из результатов изучения кинетики их протекания. Однако сложность расчетов (связанная с многокомпонентностью реакционных смесей, взаимным влиянием реактантов на скорости химических превращений и с погрешностью измерений) требует поиска новых подходов к математическому определению динамических параметров таких систем. Один из таких подходов представлен выше.

Работа поддержана РФФИ (грант N 03-01-00415), МинПромНауки в рамках государственного контракта N 37.011.11.0012 (доп. соглашение N 3 от 31.01.03).

Литература

1. Банди Б. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988. 128 с.

2. Иванов А.Г. Метод Монте-Карло в параллельной программе минимизации // Проблемы теоретической и прикладной математики: Труды 31-й Региональной молодежной конференции. Екатеринбург: УрО РАН, 2000. С. 127-128

Главное меню | Публикации |