А. Г. ИВАНОВ
МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ САМОЛЕТА
НА ЭТАПЕ ПОСАДКИ
В настоящее время разрабатываются и исследуются новые алгоритмы управления самолетом на взлете и посадке [2, 5-7, 9, 12, 14, 16, 17], приспособленные для работы в условиях резких порывов ветра (сдвиг ветра). Сдвиг ветра может возникать, в частности, когда самолет проходит зону микровзрыва, в которой ниспадающий поток воздуха ударяется о землю и растекается с образованием вихря [4, 11, 14 - 18].
В статье исследуется задача управления самолетом на посадке в вертикальной плоскости. Нелинейные дифференциальные уравнения движения взяты из [17], где эта задача исследуется в предположении, что параметры микровзрыва, в том числе и его геометрическое расположение, известны заранее. Такое предположение позволяет находить оптимальное управление как программное, т. е. в виде функции времени. Цель статьи -- построить управление обратной связи, удовлетворительно работающее при любом расположении микровзрыва относительно глиссады снижения. Таким образом, мы не предполагаем наличие точной априорной информации о ветровом возмущении. Достаточно ориентировочно задать лишь размах возможных колебаний скорости ветра относительно некоторого среднего значения. Для нахождения управления обратной связи использованы численные методы теории дифференциальных игр [1, 2-4, 8, 10, 11, 13].
§1. НЕЛИНЕЙНАЯ СИСТЕМА ДВИЖЕНИЯ САМОЛЕТА.
ПОСТАНОВКА ЗАДАЧИ
Математическая модель движения самолета взята из [17]. Рассматривается движение в вертикальной плоскости. В качестве возмущения используются, вертикальная и горизонтальная составляющие скорости ветра в центре масс самолета. Управление самолетом осуществляется через изменение угла атаки и силы тяги.
Основные переменные:
![]() -- воздушная скорость самолета, м/с;
-- воздушная скорость самолета, м/с;
![]() -- угол между вектором воздушной скорости и горизонтальной осью, рад;
-- угол между вектором воздушной скорости и горизонтальной осью, рад;
![]() -- горизонтальная координата, м;
-- горизонтальная координата, м;
![]() -- вертикальная координата, м;
-- вертикальная координата, м;
![]() и
и ![]() -- горизонтальная и вертикальная компоненты скорости ветра
в точке нахождения самолета, м/с;
-- горизонтальная и вертикальная компоненты скорости ветра
в точке нахождения самолета, м/с;
![]() -- угол атаки, рад;
-- угол атаки, рад;
![]() -- угол между осью двигателей и продольной осью самолета, рад;
-- угол между осью двигателей и продольной осью самолета, рад;
![]() -- масса самолета, кг;
-- масса самолета, кг;
![]() -- ускорение свободного падения, м/с2,
-- ускорение свободного падения, м/с2,
![]() -- сила тяги, Н;
-- сила тяги, Н;
![]() -- аэродинамическое сопротивление, Н;
-- аэродинамическое сопротивление, Н;
![]() -- подъемная сила, Н;
-- подъемная сила, Н;
![]() -- коэффициент установки тяги;
-- коэффициент установки тяги;
![]() -- плотность воздуха, кг/м3;
-- плотность воздуха, кг/м3;
![]() -- эффективная площадь самолета, м2.
-- эффективная площадь самолета, м2.
В нелинейную модель входят два основных динамических уравнения
и два кинематических:
Предполагается, что поле скорости ветра стационарно, поэтому производные
по времени от компонент ![]() ,
, ![]() удовлетворяют соотношениям
удовлетворяют соотношениям
Заданы также функциональные соотношения
![]() ,
,
![]() ,
,
![]() . Выражение для силы тяги имеет
вид
. Выражение для силы тяги имеет
вид
Здесь ![]() -- коэффициент установки тяги;
-- коэффициент установки тяги; ![]() -- стандартная тяга.
Коэффициенты
-- стандартная тяга.
Коэффициенты ![]() ,
, ![]() ,
, ![]() зависят от высоты взлетно-посадочной
полосы (ВПП) над уровнем моря и окружающей температуры.
Аэродинамическое сопротивление и подъемная сила берутся в виде
зависят от высоты взлетно-посадочной
полосы (ВПП) над уровнем моря и окружающей температуры.
Аэродинамическое сопротивление и подъемная сила берутся в виде
Коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() зависят от положения
закрылков и шасси,
зависят от положения
закрылков и шасси, ![]() -- заданная константа.
-- заданная константа.
Фазовыми переменными в модели являются
![]() и
и ![]() .
Управляющие параметры -- угол атаки
.
Управляющие параметры -- угол атаки ![]() и коэффициент установки тяги
и коэффициент установки тяги
![]() . Ограничения:
. Ограничения:
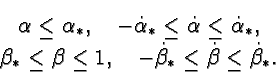
Здесь
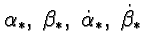 -- фиксированные числа. Для реализации ограничений на производные в
[17] применяется специальный прием с использованием тригонометрических
функций. В данной статье ограничения на производные
-- фиксированные числа. Для реализации ограничений на производные в
[17] применяется специальный прием с использованием тригонометрических
функций. В данной статье ограничения на производные ![]() и
и
![]() введены при помощи дополнительных соотношений:
введены при помощи дополнительных соотношений:
По смыслу задачи управляющие воздействия
![]() следует выбирать так, чтобы отклонение самолета от прямолинейной
глиссады снижения в процессе движения было возможно меньше. Прн этом
самолет проходит через зону ветрового возмущения, вызванного микровзрывом.
В [17] структура микровзрыва и его расположение предполагались заранее
известными. Мы будем считать, что такая информация отсутствует. Закон
управления по принципу обратной связи будет найден из решения
вспомогательной линейной дифференциальной игры аналогично тому, как
описано в [2-4, 10, 11]. Эффективность полученного способа управления
исследуется затем при моделировании движений исходной нелинейной системы
(1.1)-(1.6). Изменение ветра задается при помощи модели
микровзрыва из [17].
следует выбирать так, чтобы отклонение самолета от прямолинейной
глиссады снижения в процессе движения было возможно меньше. Прн этом
самолет проходит через зону ветрового возмущения, вызванного микровзрывом.
В [17] структура микровзрыва и его расположение предполагались заранее
известными. Мы будем считать, что такая информация отсутствует. Закон
управления по принципу обратной связи будет найден из решения
вспомогательной линейной дифференциальной игры аналогично тому, как
описано в [2-4, 10, 11]. Эффективность полученного способа управления
исследуется затем при моделировании движений исходной нелинейной системы
(1.1)-(1.6). Изменение ветра задается при помощи модели
микровзрыва из [17].
В расчетах использовали следующие численные значения:
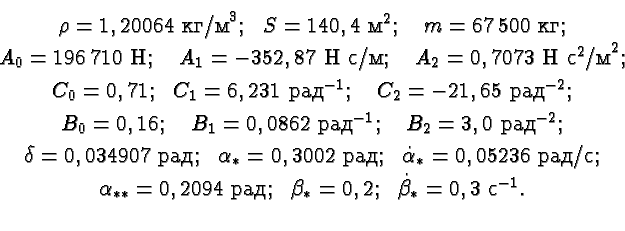
§2. МОДЕЛЬ МИКРОВЗРЫВА
В [17] модель микровзрыва описывается соотношениями
где коэффициент ![]() характеризует интенсивность микровзрыва;
характеризует интенсивность микровзрыва;
![]() -- фиксированная высота (300 м); функции
-- фиксированная высота (300 м); функции ![]() заданы
графически. В данной работе использовали зависимости
заданы
графически. В данной работе использовали зависимости
графики которых близки к приведенным в [17]. Символ ![]() означает расстояние
до центра микровзрыва.
означает расстояние
до центра микровзрыва.
§3. ЛИНЕЙНАЯ СИСТЕМА
Линейная система для вспомогательной дифференциальной игры получена путем
линеаризации исходной нелинейной системы относительно номинального
равномерного движения по прямолинейной глиссаде при нулевом ветре.
Ограничения на производную величины ![]() в линейной системе не вводятся.
Приняты следующие обозначения:
в линейной системе не вводятся.
Приняты следующие обозначения:
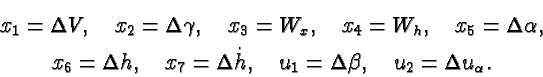
Система имеет вид
Здесь ![]() означает производную
означает производную ![]() по
по ![]() в номинальном режиме,
аналогичный смысл имеет
в номинальном режиме,
аналогичный смысл имеет ![]() и т. д.; коэффициент
и т. д.; коэффициент ![]() задает инерционность изменения угла атаки; инерционность изменения
составляющих скорости ветра определяется коэффициентом
задает инерционность изменения угла атаки; инерционность изменения
составляющих скорости ветра определяется коэффициентом ![]() ;
управляющими параметрами в системе (3.1) являются
;
управляющими параметрами в системе (3.1) являются ![]() ;
воздействие помехи определяется параметрами
;
воздействие помехи определяется параметрами ![]() .
.
В качестве номинального движения взято равномерное движение со скоростью
![]() м/с при нулевом ветре по прямолинейной глиссаде с углом наклона
м/с при нулевом ветре по прямолинейной глиссаде с углом наклона
![]() рад.
Получаемые при этом номиналы угла атаки и коэффициента установки тяги
имеют значения
рад.
Получаемые при этом номиналы угла атаки и коэффициента установки тяги
имеют значения
![]() рад,
рад,
![]() . Номинальное значение
. Номинальное значение ![]() управляющего
воздействия
управляющего
воздействия ![]() совпадает с
совпадает с ![]() .
Коэффициент
.
Коэффициент ![]() взят равным 0,2;
взят равным 0,2;
![]() .
.
Численный вид линейной системы (3.1):
§4. ВСПОМОГАТЕЛЬНАЯ ЛИНЕЙНАЯ ДИФФЕРЕНЦИАЛЬНАЯ ИГРА
Систему линейных дифференциальных уравнений (3.3) запишем в векторной форме:
Условимся, что воздействия ![]() принадлежат первому игроку,
принадлежат первому игроку,
![]() -- второму. Считаем их ограниченными по модулю:
-- второму. Считаем их ограниченными по модулю:
Введем функцию платы ![]() , зависящую от координат
, зависящую от координат ![]() и
и
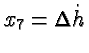 . Для этого рассмотрим на плоскости
. Для этого рассмотрим на плоскости ![]() выпуклый
шестиугольник
выпуклый
шестиугольник ![]() , симметричный относительно нуля. Его вершины:
(-3, 0), (-3, 1), (0, 1), (3, 0), (3, -1), (0, -1). Положим
, симметричный относительно нуля. Его вершины:
(-3, 0), (-3, 1), (0, 1), (3, 0), (3, -1), (0, -1). Положим
Множество ![]() можно трактовать как допуск на отклонения
можно трактовать как допуск на отклонения ![]() ,
,
![]() . Функция
. Функция ![]() показывает отклонение от допуска.
показывает отклонение от допуска.
Рассмотрим антагонистическую дифференциальную игру с динамикой (4.1),
фиксированным моментом окончания ![]() и платой
и платой ![]() . Первый игрок
минимизирует значение платы
. Первый игрок
минимизирует значение платы ![]() в момент
в момент ![]() , второй -- максимизирует.
Примем
, второй -- максимизирует.
Примем ![]() с. Оптимальная стратегия первого игрока в игре
(4.1)--(4.3) будет использована для задания управления
движением самолета в исходной нелинейной системе (1.1)--(1.6).
с. Оптимальная стратегия первого игрока в игре
(4.1)--(4.3) будет использована для задания управления
движением самолета в исходной нелинейной системе (1.1)--(1.6).
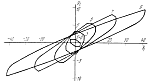 Рис. 1 |
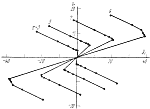 Рис. 2 |
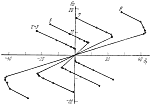 Рис. 3 |
§5. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Общая схема моделирования соответствует описанной в [3, 4, 10, 11].
Ветровое возмущение формируется при помощи модели микровзрыва
(2.1), (2.2), где параметр ![]() взят равным 1,2.
При этом продольная составляющая скорости ветра меняется вдоль движения
самолета от
взят равным 1,2.
При этом продольная составляющая скорости ветра меняется вдоль движения
самолета от ![]() до
до ![]() м/с. Вертикальная составляющая зависит от высоты,
на которой самолет проходит зону микровзрыва.
м/с. Вертикальная составляющая зависит от высоты,
на которой самолет проходит зону микровзрыва.
Начальное положение самолета брали равным 5500 м от торца ВПП по горизонтали
и 300 м над поверхностью земли. При угле наклона глиссады ![]() номинальная высота над торцом ВПП составляет 11,76 м. Начальные условия
номинальная высота над торцом ВПП составляет 11,76 м. Начальные условия
![]() ;
;
![]() рад;
рад;
![]() рад для системы
(1.1)--(1.6) соответствует движению по глиссаде с заданной
воздушной скоростью
рад для системы
(1.1)--(1.6) соответствует движению по глиссаде с заданной
воздушной скоростью ![]() м/с при продольном ветре
м/с при продольном ветре ![]() м/с и
нулевом вертикальном ветре (до входа в зону микровзрыва продольный ветер
постоянен и равен
м/с и
нулевом вертикальном ветре (до входа в зону микровзрыва продольный ветер
постоянен и равен ![]() м/с, вертикальный ветер отсутствует).
м/с, вертикальный ветер отсутствует).
Построение движения проводили до наступления одного из двух событий:
а) удара о землю (![]() ); б) пролета торца ВПП (
); б) пролета торца ВПП (![]() м).
Управления
м).
Управления ![]() ,
, ![]() формировали при помощи линий
переключения, полученных из решения вспомогательной дифференциальной
игры (4.1)--(4.3). Для каждой компоненты
формировали при помощи линий
переключения, полученных из решения вспомогательной дифференциальной
игры (4.1)--(4.3). Для каждой компоненты ![]() ,
,
![]() использовали блок из 200 линий переключения,
построенных на промежутке 10 с с шагом 0,05 с. Линию переключения
выбирали на основе оценки времени, оставшегося до момента пролета торца ВПП.
А именно, пусть
использовали блок из 200 линий переключения,
построенных на промежутке 10 с с шагом 0,05 с. Линию переключения
выбирали на основе оценки времени, оставшегося до момента пролета торца ВПП.
А именно, пусть ![]() -- время до пролета, соответствующее
номинальной скорости.
-- время до пролета, соответствующее
номинальной скорости.
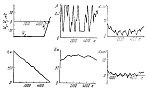 Рис. 4 |
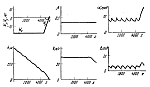 Рис. 5 |
Результаты моделирования, проведенного на ЭВМ БЭСМ-6, представлены на
рис. 4--9. Всюду по горизонтали откладывается пройденное расстояние.
Линейные величины взяты в метрах, угловые -- в градусах,
![]() -- угол тангажа. Рассмотрены три варианта
-- угол тангажа. Рассмотрены три варианта
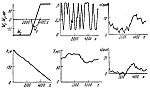 Рис. 6 |
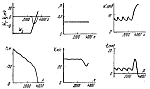 Рис. 7 |
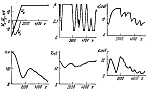 Рис. 8 |
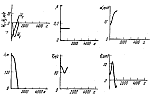 Рис. 9 |
Сравнивая полученные траектории с результатами моделирования, приведенными в [17], отметим, что они аналогичны в случае, когда отклонение скорости вертикального ветра от номинального нулевого значения не превышает 8 м/с (перепад горизонтального ветра во всех вариантах моделирования в данной работе один и тот же). Когда вертикальный ветер достигал 17 м/с, это отклонение существенно превышало величины, приведенные в [17]. Результаты моделирования показывают также значительное влияние тяги на процесс управления: управление с постоянной тягой явно неудовлетворительно. Аналогичный вывод следует из статьи [17].
С П И С О К Л И Т Е Р А Т У Р Ы
1. Алгоритмы и программы решения линейных дифференциальных игр (материалы по математическому обеспечению ЭВМ). Свердловск: УНЦ АН СССР, 1984.
2. Боткин Н. Д., Кейн В. М., Пацко В. С. Модельная задача об управлении боковым движением самолета на посадке // ПММ. 1984. Т. 48, вып. 4. С. 560-567.
3. Боткин Н. Д., Кейн В. М., Пацко В. С. Применение методов теории дифференциальных игр к задаче управления самолетом на посадке // Позиционное управление с гарантированным результатом. Свердловск, 1988. С. 33-44.
4. Боткин Н. Д., Keйн В. М., Пацко В. С., Турова В. Л. Управление самолетом на посадке при сдвиге ветра // ПУТИ. 1989. Т. 18, N 4. С. 223-235.
5. Боткин Н. Д., Красов А. И. Позиционное управление в модельной задаче о разбеге самолета // Позиционное управление с гарантированным результатом. Свердловск, 1988. С. 22-32.
6. Кейн В. М., Париков А. Н., Смуров М. Ю. Об одном способе оптимального управления по методу экстремального прицеливания // ПММ. 1980. Т. 44, вып. 3. С. 434-440.
7. Корнеев В. А., Меликян А. А., Титовский И. Н. Стабилизация глиссады самолета при ветровых возмущениях в минимаксной постановке // Изв. АН СССР. ТК. 1985. N 3. С. 132-139.
8. Красовский Н. Н., Субботин А. И. Позиционные дифференциальные игры. М.: Наука, 1974.
9. Кузьмин В. П., Ярошевский В. А. Оценка предельных отклонений параметров траекторий самолета при автоматической посадке // Уч. зап. ЦАГИ, 1984. Т. 15, N 2. С. 43-56.
10. Боткин Н. Д., Пацко В. С. Применение методов теории дифференциальных игр для имитации ветрового возмущения // Разработка численных методов построения экстремальных ветровых возмущений, действующих на самолет на этапе посадки. Свердловск: ИММ УрО АН СССР, 1987. 46 с. Отчет о НИР ГР N 1880003467. Инв. N 02880044271.
11. Боткин Н. Д., Пацко В. С., Турова В. Л. Разработка алгоритмов построения экстремальных ветровых возмущений // Разработка численных методов построения экстремальных ветровых возмущений, действующих на самолет на этапе посадки. Свердловск: ИММ УрО АН СССР, 1987. 57 с. Отчет о НИР ГР N 1880003467. Инв. N 02880054701.
12. Титовский И. Н. Игровой подход к задаче синтеза управления самолетом при заходе на посадку // Уч. зап. ЦАГИ. 1981. Т. 12, N 1. С. 85-92.
13. Боткин Н. Д., Кейн В. М,, Красов А. И., Пацко В. С. Управление боковым движением самолета на посадке в условиях ветрового возмущения // Исследование по совершенствованию бортовых и наземных автоматизированных систем управления воздушными судами. ОЛАГА, 1983. 78 с. Отчет о НИР ГР N 81104592. Инв. N 0283007880,
14. Chen Y. Н., Раndеу S. Robust Control Strategy for Take-Оff Performance in а Windshear // Opt. Control Appl. Methods. 1989. V. 1О. P. 65-79.
1б. Ivаn M. А Ring-Vortex Downburst Model for Flight Simulation // J. Aircraft. 1986. V. 23, N 3. Р. 232-236.
16. Мielе А., Wаng T., Melvin W. W. Optimal Take-Off Trajectories in the Presence of Windshear // J. Opt. Theory Appl. 1986. V. 49, N 1. Р. 1-45.
17. Miele A., Wаng T., Wаng H., Меlvin W. W. Optimal Penetration Landing Trajectories in the Presence of Windshear // Ibid. 1988. V. 57, N 1. Р. 1-40.
18. Рsiаki М. L., Stеngеl R. F. Optimal Flight Path Through Microburst Wind Profiles // J. Aircraft. 1986. V. 23, N 8. Р. 629-635.
Статья восстановлена путем сканирования печатного издания. Исправлено несколько опечаток.
©УрО РАН, 1992
©Алексей Иванов, 1992
©IAGSoft, 2000

Иванов А.Г. Моделирование движения самолета на этапе посадки. В кн.: Проблемы управления с гарантированным результатом. Екатеринбург, 1992. С.15-26.
|
Главное меню | Публикации | Электронные публикации | Обо мне |
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru