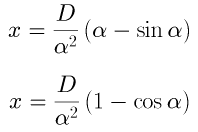
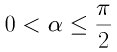
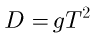Иванов Алексей Геннадьевич

Классическая задача о брахистохроне

Копаем помаленьку Ведутся работы

Проблема нахождения произвольных постоянных при различных краевых условиях

Нахождение амплитуды циклоиды A и верхней границы параметра \alpha при заданной конечной точке (x1, y1) требует нахождения корня трансцендентного уравнения. Для этого приходиться применять численные методы

Страница с апплетом на JAVA - изображает брахистохрону для указанных пользователем граничных условий (версия страницы для медленных компьютеров с видеорежимом 640x480). Старая версия апплета находится здесь.

Изохроны в задаче о брахистохроне

Изохроны (линии равного оптимального времени) в классической задаче о брахистохроне можно выписать аналитически в параметрической форме:

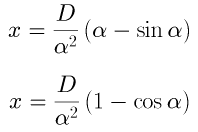
$$x=\frac{D}{\alpha^2}\left(\alpha-\sin\alpha\right)$$$$x=\frac{D}{\alpha^2}\left(1-\cos\alpha\right)$$
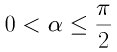
$$0<\alpha\leq\frac{\pi}{2}$$
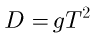$$D=2 g T^2$$,

где 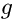$g$ - ускорение свободного падения, 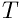$T$ - время, соответствующее изохроне.

На небольшом рисунке справа изображены изохроны. Доступен большой рисунок. изохроны
Копаем помаленьку Ведутся работы
Vari Home ElePub I
Вариационное исчисление | Домашняя страница | Электронные публикации | Печатные работы
Пишите по адресу: iagsoft@imm.uran.ru