Задача о брахистохроне в центральном поле тяготения является модификацией
классической задачи о брахистохроне
(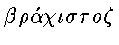 - кратчайший,
- кратчайший,
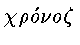 - время ), предложенной в 1696г. Иоганном
Бернулли и сыгравшей большую роль в развитии вариационного исчисления.
- время ), предложенной в 1696г. Иоганном
Бернулли и сыгравшей большую роль в развитии вариационного исчисления.
1. Классическая задача о брахистохроне
Пусть даны две точки, расположенные на разной высоте и не
лежащие на одной вертикальной прямой. Проведем через данные точки вертикальную
плоскость и рассмотрим кривые, соединяющие эти точки и расположенные в данной
плоскости. Из этих кривых выберем такие, что материальная точка единичной
массы, выходящая из верхней точки P со скоростью v0 = 0, двигаясь только
под действием силы тяжести, достигнет нижней точки Q.
Задача о брахистохроне формулируется следующим образом:
- Существует ли среди этих кривых такая, которую точка пробегает за
минимальное время?
- Если такая кривая существует, то как ее найти?
Формализуем данную задачу.
Выберем в вертикальной плоскости, определенной двумя данными точками,
прямоугольную систему координат так, чтобы точка P совпала с началом координат,
а ось Oy направим вертикально вниз. Пусть точка Q имеет
координаты (x1, y1) (рис.1).
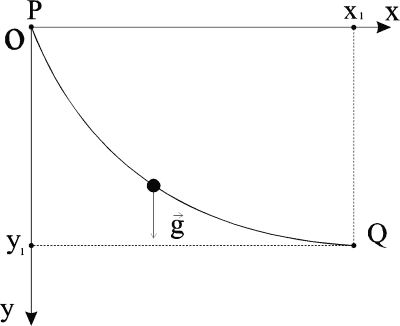
Рис.1
Для простоты предположим, что рассматриваются только такие кривые,
которые являются графиками функций y, где
y 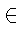 (R1
(R1 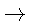 R1)
R1)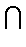 C1[0, x1].
Итак, выберем такую функцию y, которая удовлетворяет граничному условию
C1[0, x1].
Итак, выберем такую функцию y, которая удовлетворяет граничному условию
y(0) = 0, y(x1) = y1.
В этом случае время
T = T[y( . )], необходимое
материальной точке для движения вдоль кривой, которая является графиком
функции
y = y(x) (x 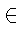 [0, x1]), выражается следующей формулой:
(g - ускорение свободного падения).
Сформулированная проблема приводит к исследованию на экстремум
функционала
T[y( . )] .
[0, x1]), выражается следующей формулой:
(g - ускорение свободного падения).
Сформулированная проблема приводит к исследованию на экстремум
функционала
T[y( . )] .
2. Постановка задачи о брахистохроне в центральном поле тяготения
Пусть даны две точки P и Q, расположенные в центральном поле тяготения.
Проведем через точки P и Q и центр тяготения
плоскость и рассмотрим кривые, соединяющие эти точки и расположенные в данной
плоскости. Из этих кривых выберем такие, что материальная точка единичной
массы, выходящая из точки P со скоростью v0 = 0, двигаясь только
под действием центральной силы, достигнет точки Q.
Задача о брахистохроне формулируется следующим образом:
- Существует ли среди этих кривых такая, которую точка пробегает за
минимальное время?
- Если такая кривая существует, то как ее найти?
Формализуем данную задачу.
Задача о брахистохроне в центральном поле тяготения имеет следующие отличия от
классической задачи:
- Сила тяжести, под действием которой двигается материальная
точка, является центральной силой тяжести.
- Сила тяжести не постоянна:
|
F| =
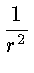
,
Исследование данной задачи и вывод функционала времени движения удобно
проводить в полярной системе координат, причем без ограничения общности
можно упростить постановку задачи.
Рассмотрим центральное поле тяготения на плоскости с центром в точке O.
Пусть на плоскости дан круг B радиуса r0 с центром в точке O.
Рассмотрим две точки P, Q 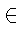 B, причем
P
B, причем
P 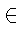
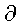 B. Введем полярную
систему координат (
B. Введем полярную
систему координат (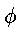 , r) с центром в точке O так, чтобы точка P
имела координаты (0, r0). Пусть точка Q имеет координаты
(
, r) с центром в точке O так, чтобы точка P
имела координаты (0, r0). Пусть точка Q имеет координаты
(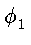 , r1) (
r1
, r1) (
r1 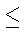 r0) (рис.2).
r0) (рис.2).
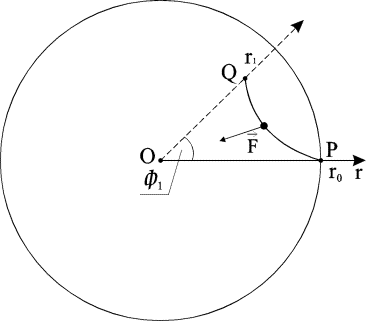
Рис.2
Для простоты предположим, что рассматриваются только такие кривые,
которые являются графиками функций r, где
r 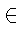 ([0, 2
([0, 2 )
) 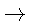 [0, r0])
[0, r0])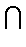 C1([0, 2
C1([0, 2 )),
причем функция r должна удовлетворять граничному условию
)),
причем функция r должна удовлетворять граничному условию
r(0) =
r0,
r(
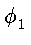
) =
r1.
3. Вывод функционала времени движения
Введем следующие обозначения:
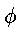 - полярный угол движущейся точки
(
- полярный угол движущейся точки
(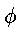
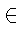 [0,
[0,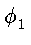 );
);
t - время,прошедшее с момента начала движения
(t 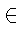 [0, T]);
[0, T]);
s -длина пути, пройденного движущейся точкой
(s 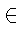 [0, S]);
[0, S]);
v - скорость движущейся точки;
K - кинетическая энергия точки;
P - потенциальная энергия точки;
F - центральная сила притяжения, действующая на точку
(| F| = 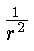 ).
Ясно, что
).
Ясно, что
v =
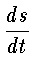
.
Будем исходить из закона сохранения энергии
K + P = const .
В нашем случае
K =
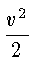
,
P = - |
F|
r = -
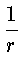
.
Следовательно, закон сохранения энергии имеет вид :
откуда с помощью простых преобразований получаем, что
v =
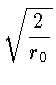
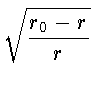
.
Дифференциал дуги в полярной системе координат выражается формулой
ds =
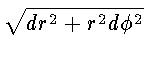
,
которую можно записать в виде
ds =
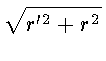 d
d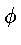
.
Тогда
dt =
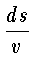
=
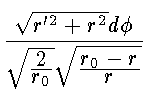
.
Интегрируя, получаем функционал
Таким образом, сформулированная задача о брахистохроне в центральном
поле тяготения приводит к исследованию на минимум функционала
T[r( . )].
Для нахождения минимума функционала
T[r( . )] имеет смысл применять
численные методы.
На рис.3 изображено поле оптимальных траекторий для r0 = r1 = 1, построенное численное.
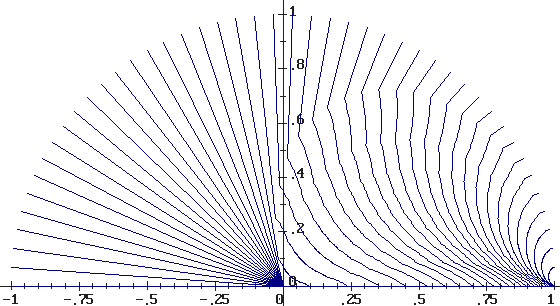
Рис.3
4. Изохроны
 Ведутся работы
Ведутся работы
На рис.4 изображены изохроны - линии равного оптимального времени.
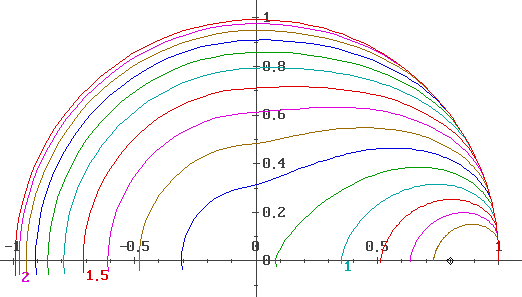 Рис.4
Рис.4
В создании этой страницы принимала участие студентка УрГУ Камнева Л.В.
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru



 .
.
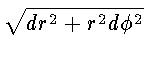 ,
,
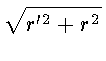 d
d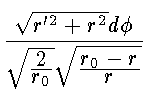 .
.
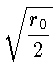
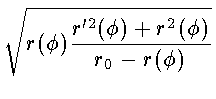 d
d
![]() Ведутся работы
Ведутся работы

 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru