Имя Исаака Ньютона присвоено одному из направлений теории гиперзвуковых течений, а именно направлению, основанному на предположении, что отношение плотностей на скачке равно нулю (предельная форма предположения Г), а ударный слой является бесконечно тонким. Прежде чем приступить к изложению этой теории, мы кратко расскажем здесь о том, что сделал Ньютон в газовой динамике и почему его имя связывается с этим разделом современной теории гиперзвуковых течений.
Исследования Ньютона, представляющие для нас интерес, были выполнены в конце семнадцатого века задолго до того, как были развиты основные положения термодинамики, кинетической теории, теории вязкости и т. д. Поэтому не удивительно, что некоторые из теорий и результатов Ньютона могут в свете современных знаний казаться ошибочными. Ньютон предложил некоторую модель взаимодействия молекул, которая служила вместо современных моделей кинетической теории. Ньютон не проводил различия между изэнтропическим процессом в звуковой волне и изотермическим процессом в медленно протекающих лабораторных опытах. Его расчеты сопротивления тел в несжимаемой жидкости были основаны на некоторой физически нереальной модели.
Ньютон не знал понятия ударной волны или ударного слоя. Он, по-видимому, не представлял себе отчетливо, что, для того чтобы при обтекании тела сжимаемость играла доминирующую роль, необходима определенная величина скорости течения. Ньютон пользовался общим дедуктивным методом. Он отправлялся от некоторой системы основных законов и некоторой гипотетической модели физической задачи и приходил к логическому решению задачи на основе этой модели. Получаемые при этом результаты позволяли давать некоторую оценку соответствия их применявшейся модели, но не всегда позволяли проверить правильность этой модели с физической точки зрения.
Критика научных результатов Ньютона, опирающаяся на наши более точные знания, накопленные за прошедшие два с половиной столетия, едва ли интересна. Но несомненный интерес представляет понимание ньютоновской системы механики материи, которая послужит основой для обсуждения замечательных дедуктивных заключений Ньютона. Цитаты из «Математических начал натуральной философии» Ньютона, которые мы будем приводить в нашем обзоре, будут даваться по изданному Кеджори английскому переводу, сделанному Эндрью Моттом с 3-го издания этого труда (см. Ньютон [1] 1). Для нас наиболее непосредственный интерес в «Началах» Ньютона представляют Предложения 32–35 (Теоремы 27 и 28, Задача 7), Отдел VII, Книга II и Замечание 35 в добавлении Кеджори. Согласно Кеджори, Предложение 35 из первого издания было напечатано во втором и третьем изданиях как Предложение 34.
Ньютону было известно, что такие газы, как воздух и пап, являются упругими и что между плотностью и давлением имеется связь, известная теперь как закон Бойля. Ньютон знал, что такие жидкости, как вода и ртуть, являются практически несжимаемыми и имеют значительно большую плотность, чем газы. Ньютону было известно также, что вода и пар являются одним и тем же веществом. Поэтому он считал, что жидкости бывают «упругие» (имеющие переменную плотность) или «неупругие», у которых плотность есть некоторое присущее данной среде неизменное свойство.
Поскольку кинетической теории тогда не существовало, Ньютон выдвинул постулат, что «отталкивательные силы» между соседними частицами упругой жидкости являются возможным механизмом, объясняющим упругость жидкости. При такой модели давление в упругой жидкости возникает прежде всего из-за действия этих отталкивательных сил. Ньютон установил, что можно получить соответствие с законом Бойля (уравнением состояния совершенного газа), если предположить, что отталкивательная сила между двумя соседними частицами обратно пропорциональна расстоянию между ними (Книга II, Предложение 23). Ньютон ввел также понятие разреженной среды, т. е. среды, которая состоит из малых частиц, находящихся на больших расстояниях друг от друга; при этом он, очевидно, сделал дополнительное предположение о том, что отталкивательными силами между такими частицами можно пренебрегать.
Мы будем рассматривать выводы Ньютона на основе модели, которую он постулировал для совершенного газа, причем мы попытаемся формулировать результаты Ньютона, пользуясь современной терминологией. Поэтому, имея в виду давление в совершенном газе, мы будем соответственно интерпретировать силы взаимодействия между частицами как обратно пропорциональные расстоянию. Оценивая результаты Ньютона, мы должны иметь в виду, что они были получены дедуктивным методом на основе гипотетической модели, согласующейся с реальным уравнением состояния газа, хотя детали этой модели нельзя сегодня считать правильными. Мы увидим, что Ньютон определенно предвосхитил понятие о подобии по числу Маха и принцип независимости от числа Маха. Ньютон получил также обширные и поучительные результаты для гиперзвуковых свободно-молекулярных течений при гипотетических условиях на поверхности тела.
В Предложении 32 Ньютон устанавливает полное подобие движений двух подобных систем частиц при условии (в указанной выше интерпретации), что давление пропорционально произведению плотности на квадрат скорости. При выводе этого утверждения Ньютон предполагает, что частицы не действуют одна на другую «ни с какими силами, за исключением ускорительных сил, обратно пропорциональных линейным размерениям соответствующих частиц и прямо пропорциональных квадратам их скоростей». Читатель может заметить, что произведение ускорения на расстояние имеет ту же размерность, что и давление, деленное на плотность.
В Предложении 33 Ньютон распространяет это подобие на сопротивление тела в среде, состоящей из таких частиц. Его условие подобия можно перефразировать следующим образом: скорость тела должна быть пропорциональна скорости звука (в ньютоновском определении скорости звука). Следовательно, результат Ньютона можно выразить так: коэффициент сопротивления тела данной формы в подобных сжимаемых жидкостях зависит только от числа Маха. Сам же Ньютон специально не связывал условие подобия со скоростью звука. Можно отметить, что Кранц [2, стр. 45] вывел подобие по числу Маха именно из ньютоновского подобия.
В Следствии 2 Предложения 33 Ньютон замечает сначала, что «в среде, частицы которой, находящиеся в некотором расстоянии друг от друга, совсем не оказывают взаимодействий, сопротивление в точности пропорционально квадрату скорости». Этот случай соответствует нашему предельному случаю бесконечного числа. Маха в среде с абсолютной температурой, равной нулю. Используя это соображение, Ньютон показывает, что при очень большой скорости силами отталкивания (или давлением) можно пренебрегать.
В Следствии 3 Ньютон повторяет свое заключение: «Сопротивление тела, движущегося весьма быстро во всякой упругой жидкости, почти такое же, как если бы частицы жидкости были лишены отталкивательных сил; в упругих жидкостях сила упругости происходит от отталкивательных сил частиц, и надо, чтобы скорость была настолько велика, чтобы эти силы не имели достаточно времени, чтобы проявить свое действие». В этих двух Следствиях Ньютон излагает для совершенного газа, который он рассматривает, принцип, эквивалентный принципу независимости от числа Маха, или подобию по Осватичу.
В Предложениях 34 и 35 Ньютон рассматривает разреженную среду, для которой он, естественно, постулирует отсутствие взаимодействия между отдельными частицами и рассматривает лишь силу соударения между телом и частицами, находящимися в пространстве, через которое движется тело. В Предложении 34 Ньютон принимает (однако не явным образом), что закон соударения, определяющий потерю нормальной составляющей количества движения, не зависит от угла встречи частицы с поверхностью тела и что при ударе не происходит изменения касательной составляющей количества движения. Таким образом, Ньютон заключает, что импульс (сила удара частицы о тело) пропорционален синусу угла встречи и направлен по нормали к телу. Составляющая этого импульса от одной частицы, влияющая на сопротивление, пропорциональна квадрату синуса угла встречи.
В Поучении к Предложению 34 Ньютон определяет форму тела с заданной длиной и заданным диаметром кормового среза, которое в соответствии с его моделью имеет минимальное сопротивление. Вычисления Ньютона, приводящие к этому результату, были обнаружены в его переписке и, как указывает Кеджори, представляют собой самое раннее решение некоторой задачи вариационного исчисления. Современный вывод этого решения Ньютона вместе с экспериментальными результатами для таких оптимальных тел можно найти в статье Эггерса, Резникова и Денниса [1].
В Предложении 35 Ньютон рассчитал сопротивление сферы для различных законов соударения. В Случае 1 он рассмотрел абсолютно упругое соударение, а в Случае 2 — абсолютно неупругое соударение (для нормальной составляющей количества движения). Сопротивление сферы в Случае 1 просто равняется удвоенному сопротивлению в Случае 2. Для свободно-молекулярных течений ньютоновский Случай 1 соответствует зеркальному отражению, когда все коэффициенты аккомодации равны нулю. Случай 2 соответствует такому отражению, когда коэффициент аккомодации для касательной составляющей количества движения (или касательного напряжения) равен нулю, а коэффициент аккомодации для нормальной составляющей количества движения (или давления) равен единице, что имеет место в том случае, когда тело является очень холодным; если же тело не является холодным, то коэффициент аккомодации для нормальной составляющей количества движения должен быть больше единицы.
За исключением результатов, полученных для нормальной составляющей количества движения (или давления) в Случае 2, ни один из ньютоновских случаев вообще не может рассматриваться как физически реальный, потому что для действительных разреженных течений температура тела не существенна. Физически нереальная модель зеркального отражения в современных теоретических исследованиях рассматривается иногда как интересный частный случай.
Однако решение Ньютона может быть реальным для течений при высоких числах Маха
с большой плотностью и существенно невязким ударным слоем. При очень большом
числе Маха среда перед скачком является по существу разреженной средой и
становится континуумом только в ударном слое. Если ударный слой очень тонок,
то скачок имеет примерно тот же угол наклона, что и тело, а нормальная
составляющая количества движения ударяющейся молекулы теряется так же, как при
неупругом соударении, и передается телу через ударный слой. Если в ударном
слое вязкость отсутствует, то касательная составляющая количества движения
ударяющейся молекулы будет сохраняться. Для того чтобы ударный слой был
достаточно тонким, необходимо выполнение сильной формы предположения Г о малой
величине отношения плотностей на скачке
![]()
![]() 1, которое обсуждалось ранее.
Этот имеющий место на практике случай соответствует ньютоновскому Случаю 2.
1, которое обсуждалось ранее.
Этот имеющий место на практике случай соответствует ньютоновскому Случаю 2.
Эпштейн [1] был первым, кто получил газодинамическим методом формулу для давления, соответствующую ньютоновскому Случаю 2:
|
ps - p∞ = |
(3.1.1) |
Хотя указанные выше авторы были первыми, кто на основе современной теории косых скачков получил закон, выражающий давление через квадрат синуса угла наклона, однако ученым-баллистикам этот закон был известен на много лет раньше (см. Кранц [1, § 12]). Ученые-баллистики пользовались этим законом эмпирически, вводя при этом неизвестный постоянный множитель. Они рассматривали ньютоновский закон лишь как один из возможных эмпирических законов. Сам Ньютон, несомненно, внес фундаментальный вклад в баллистику, и ученые-баллистики, вероятно, были хорошо знакомы с результатами Ньютона еще со времени опубликования «Начал». Во всяком случае, связь закона, выражающего давление через квадрат синуса угла наклона тела, с именем Ньютона существовала по крайней мере в течение тридцати лет, а возможно, и больше.
Формула для давления (3.1.1) справедлива в предельном случае нулевого отношения плотностей на скачке и при условии, что форму скачка и форму тела можно считать одинаковыми. Отметим, что формула (3.1.1) дает величину давления непосредственно за скачком. Это давление равно давлению на теле только в том случае, когда после столкновения с ударным слоем каждая частица движется без ускорения или, в сущности, по свободной траектории, что находится в соответствии с моделью для ньютоновского Случая 2. Это имеет место в случае обтекания клина или конуса при нулевом угле атаки.
При обтекании тела с криволинейным контуром частица, находясь в континуальном потоке в ударном слое, вынуждена двигаться по криволинейной траектории. Поэтому должны быть приняты во внимание силы, которые требуются для искривления траекторий частиц. В результате будет иметь место изменение давления поперек ударного слоя. Это изменение давления равно потоку количества движения в этом слое, умноженному на кривизну слоя. Необходимость такой поправки, учитывающей центробежную силу при вычислении давления на поверхности тела, была установлена Буземаном [1, стр. 276–277], который дал формулу для этой поправки. Для выпуклого тела давление на поверхности тела меньше, чем давление, определяемое формулой (3.1.1), и может уменьшиться до нуля в некоторой точке на поверхности тела, где эта поверхность еще имеет положительный угол наклона относительно направления невозмущенного потока.
Учет поправки Буземана на центробежные силы необходим для построения логичной гиперзвуковой теории, которая была бы точна в предельном смысле. Лиз [3, раздел (4)] на основании опытов предложил «модифицированную ньютоновскую формулу», выражающую давление через квадрат синуса угла наклона тела без поправки на центробежные силы. Эта формула теперь является общепринятой для сравнения с экспериментом.
Модификация формулы (3.1.1) заключается во введении некоторого множителя, за счет которого эта формула дает точное значение давления торможения, а вычисляемое давление при этом рассматривается как давление на теле. Эта формула полезна потому, что она несложна для расчетов и дает простую базу для сравнений. Однако она не опирается на какую-либо рациональную теорию, и следует иметь в виду ее эмпирическое происхождение.
После того как мы выяснили, что в рациональной теории гиперзвукового течения для определения давления на теле должна учитываться поправка на центробежные силы, можно уделить немного внимания вопросам терминологии. Обычно соответствующую формулу называют «формулой Ньютона с учетом центробежных сил» или «уточненной формулой Ньютона». Более логичным и подходящим было бы применение термина «формула Ньютона-Буземана».
Когда мы в этой книге будем говорить о рациональной гиперзвуковой теории с учетом поправки Буземана, то для простоты будем употреблять термин «теория Ньютона», а термином «формула Ньютона-Буземана» мы будем пользоваться для обозначения уточненной формулы для давления. Поскольку мы здесь в основном интересуемся теорией гиперзвуковых течений, то мы должны иметь в виду, что формула Ньютона для расчета давления на поверхности тела является приближенной.
Главным допущением, которое лежит в основе теории Ньютона, является сильная
или предельная форма предположения Г о малом отношении плотностей на ударной
волне. Однако реальные газы, даже те, в которых диссоциация играет
существенную роль, характеризуются такими значениями
![]() , квадратный корень
из которых нельзя считать малой величиной. Поэтому теория Ньютона в лучшем
случае дает лишь очень грубую картину реальных гиперзвуковых течений. Значит,
весьма маловероятно, что мы сможем непосредственно применять многие из
результатов, которые будут получены в этой главе. Результаты, излагаемые в
последующих четырех главах, дадут нам некоторое представление о том, какое
значение имеет применение теории Ньютона для гиперзвуковых течений.
, квадратный корень
из которых нельзя считать малой величиной. Поэтому теория Ньютона в лучшем
случае дает лишь очень грубую картину реальных гиперзвуковых течений. Значит,
весьма маловероятно, что мы сможем непосредственно применять многие из
результатов, которые будут получены в этой главе. Результаты, излагаемые в
последующих четырех главах, дадут нам некоторое представление о том, какое
значение имеет применение теории Ньютона для гиперзвуковых течений.
Прежде чем заниматься подробным анализом ньютоновской теории обтекания, уместно выяснить, представляет ли эта теория при изучении гиперзвуковых течений нечто большее, чем академический интерес.
Мы рассматриваем ньютоновскую теорию обтекания по двум основным причинам.
Первая причина состоит в том, что в одном весьма перспективном направлении в
исследовании течений около затупленных тел произвольной формы используется
метод разложения по степени отношения плотностей
![]() , а нулевое приближение в
этом методе представляет собой ньютоновское приближение. Чтобы пользоваться
каким-нибудь методом, основанным на разложении в ряды, надо, конечно, подробно
изучить нулевое приближение.
, а нулевое приближение в
этом методе представляет собой ньютоновское приближение. Чтобы пользоваться
каким-нибудь методом, основанным на разложении в ряды, надо, конечно, подробно
изучить нулевое приближение.
Вторая причина состоит в том, что рассмотрение логических следствий
ньютоновской теории может пролить свет. на некоторые явления, имеющие место в
реальных газовых течениях. Многие из логических следствий ньютоновской теории
являются аномальными, в них могут встречаться бесконечная масса, нулевое
давление, сосредоточенная сила, многократное уплотнение вещества. Наличие этих
аномальностей, конечно, связано с предельным переходом
![]()
![]() 0 (предельной
формой предположения Г).
0 (предельной
формой предположения Г).
Эти, очевидно, физические совершенно нереальные аномальные явления могут иметь важные аналоги в гиперзвуковых течениях газа. Понимание первых из упомянутых явлений необходимо для понимания вторых. Значит, не следует избегать рассмотрения этих аномальных следствий теории Ньютона, а надо выявлять их для того, чтобы обнаружить явления, которые могут быть существенными в гиперзвуковых течениях, но не имеют аналогов в течениях с умеренными скоростями. Кроме того, методы, развитые в теории Ньютона, могут указать на применение аналогичных методов в более точных теориях. Примером этого является полученное в § 4.5 решение с постоянной плотностью при наличии поперечного течения, для нахождения которого был применен метод, непосредственно подсказанный методом, изложенным в § 3.6.
Ньютоновская теория обтекания основана на концепции бесконечно тонкого ударного слоя, который совпадает с поверхностью тела, и на предположении о том, что между этим слоем и поверхностью тела отсутствует трение. На основании этих предположений и без какой-либо дальнейшей детализации структуры ударного слоя мы сможем получить формулы для давления и сил в установившемся движении для плоских и осесимметричных тел при соответствующем ограничении их формы.
Однако, вообще говоря, бывает желательно или необходимо знание структуры тонкого ударного слоя. Для этой цели нам потребуется более детально определить характер ударного слоя. В принципе можно создать много моделей ударного слоя или постулировать много правил, определяющих структуру и характер этого слоя. Все они должны согласовываться с основной гипотезой о том, что между ударным слоем и поверхностью тела отсутствует трение. Мы находим удобным рассматривать здесь три различные умозрительные модели для структуры ударного слоя, причем первые две являются в сущности идентичными. В нашем исследовании структуры ударного слоя мы будем почти исключительно пользоваться первой моделью. Мы будем рассматривать следующие модели.
А. Модель ламинарного слоя. В этой модели, которую мы будем рассматривать как стандартную в ньютоновской теории обтекания, считается, что ударный слой состоит из бесконечно большого числа независимых элементарных слоев. Каждый элементарный слой является бесконечно тонким, и в нем движется жидкость, которая вошла в ударный слой в некоторой точке. Между этой точкой входа и исследуемой точкой в ударном слое жидкость движется вдоль некоторой линии с нулевой геодезической кривизной, расположенной на поверхности тела или ударного слоя. Такая линия, как известно, называется геодезической.
В этой модели последовательность элементарных слоев в ударном слое, отсчитываемая от тела к скачку, дает нам некоторую шкалу, с помощью которой мы сможем определить частицу жидкости по ее точке входа в ударный слой. Иначе говоря, мы будем в состоянии установить взаимно однозначное соответствие между отдельными элементарными слоями внутри ударного слоя и точками входа в ударный слой соответствующих линий тока.
Данный элементарный слой содержит жидкость, поступившую в него только из одного источника. Для любой данной точки, в которой исследуется структура ударного слоя, будет существовать некоторое геометрическое место соответствующих точек входа, которое мы будем называть «геометрическим местом входов линий тока» 2). Вышеупомянутое взаимно однозначное соответствие является отображением этого геометрического места на шкалу элементарных слоев.
Это описание модели относится к случаю установившегося течения. В случае неустановившегося течения надо учитывать дополнительную координату времени, и определение аналогичного геометрического места входов линий тока значительно усложняется. Этот случай будет рассмотрен в § 3.7.
Б. Модель слоя, образованного предельным совершенным газом.
В соответствии с
этой моделью мы будем считать, что среда представляет собой совершенный газ с
нулевой вязкостью, находящийся в предельном состоянии, когда
![]()
![]() 1
и
M∞
1
и
M∞ ![]() ∞.
Такая модель должна быть более реальной, чем другие модели ньютоновского
обтекания, так как она соответствует некоторому течению газа, а единственное
искусственное ограничение состоит здесь в необходимости положить
∞.
Такая модель должна быть более реальной, чем другие модели ньютоновского
обтекания, так как она соответствует некоторому течению газа, а единственное
искусственное ограничение состоит здесь в необходимости положить
![]() равным нулю.
равным нулю.
В целом эта модель ведет себя идентично стандартной модели ламинарного слоя. Основной целью рассмотрения такой модели является стремление получить, во-первых, предположительные сведения относительно того, следует ли модифицировать стандартную модель, когда она применяется к нестандартным задачам, а во-вторых, представление о том, когда (если это вообще будет иметь место) стандартная модель ламинарного слоя будет обязательно расходиться с моделью слоя, образованного предельным совершенным газом.
Эквивалентность этой модели и модели ламинарного слоя может быть установлена при помощи уравнения количества движения, которое гласит, что ускорение частицы равно градиенту давления, взятому со знаком минус и деленному на плотность. При плотности, стремящейся к бесконечности в рассматриваемом предельном случае, ускорение частицы стремится к нулю, если градиент давления остается конечным. Градиент давления в направлении, нормальном к поверхности скачка, может стремиться к бесконечности, так как слой за скачком становится бесконечно тонким; составляющая ускорения частицы в этом направлении, вообще говоря, не равна нулю, а определяется геометрией ударного слоя.
Градиент давления в направлении, параллельном поверхности скачка, зависит от перепада давления на скачке и должен оставаться конечным. Соответственно составляющая ускорения частицы, касательная к поверхности скачка, при предельном переходе стремится к нулю, а траектория частицы в ударном слое приближается к геодезической линии поверхности скачка.
При таком умозрительном предельном переходе равным образом можно рассматривать
не совершенный, а другой гипотетический газ, если для него величина
![]() и
отношение
и
отношение
![]() к скорости звука в ударном слое стремятся к нулю. Рассмотрение
такого газа дало бы еще одну модель, также эквивалентную модели ламинарного
слоя.
к скорости звука в ударном слое стремятся к нулю. Рассмотрение
такого газа дало бы еще одну модель, также эквивалентную модели ламинарного
слоя.
В. Модель однородного слоя. В этой модели ударный слой имеет в некоторой точке характерную скорость, и все вещество в слое движется с этой скоростью. Элемент жидкости, входящий в ударный слой, в этом случае сразу же приобретает скорость слоя и в то же время вносит свою долю в количество движения слоя, направленное по касательной к поверхности тела. Это приращение количества движения влияет на скорость слоя, и, таким образом, эта скорость определяется балансом количества движения.
Такая модель является физически нереальной потому, что она требует, чтобы вещество внутри ударного слоя было бесконечно вязким, а трение на стенке отсутствовало. В предельном случае для газа с очень малым числом Рейнольдса в этой модели ударного слоя требовался бы нулевой коэффициент аккомодации для касательной составляющей количества движения при столкновении молекул с поверхностью тела. Однако модель однородного ударного слоя является крайне простой и нередко позволяет легко получать результаты, сравнимые с результатами, полученными на основе других, более реальных моделей ньютоновского ударного слоя. Большинство аномальностей, которые получаются в стандартной модели ламинарного слоя, не имеет места в модели однородного слоя.
Обратимся теперь к приложениям для плоских и осесимметричных тел. Введем
функцию тока ![]() , которая для плоских течений представляет собой поток массы
через единицу ширины, а для осесимметричных течений ˜ поток массы через
единицу меридионального угла (в радианах). В набегающем потоке функция тока
будет равна для плоского течения
, которая для плоских течений представляет собой поток массы
через единицу ширины, а для осесимметричных течений ˜ поток массы через
единицу меридионального угла (в радианах). В набегающем потоке функция тока
будет равна для плоского течения
|
|
(3.2.1а) |
|
|
(3.2.1б) |
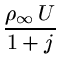 y1 + j. y1 + j.
|
(3.2.2) |
Введем также величину P, которая, если ее умножить на U, будет представлять собой количество движения в ударном слое, приходящееся на единицу ширины для плоских течений и на один радиан меридионального угла для осесимметричных течений. Изменение количества движения между двумя точками в ударном слое равно просто произведению соответствующего потока массы на касательную составляющую скорости набегающего потока. Тогда можно записать следующее равенство:
|
dP = cos |
(3.2.3) |
|
P = |
(3.2.4) |
Приращение давления, разделенное на
![]() U2, равняется половине коэффициента
давления Cp, определяемой так:
U2, равняется половине коэффициента
давления Cp, определяемой так:
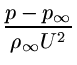 . .
|
(3.2.5) |
|
|
(3.2.6) |
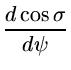 P1, P1,
|
(3.2.7) |
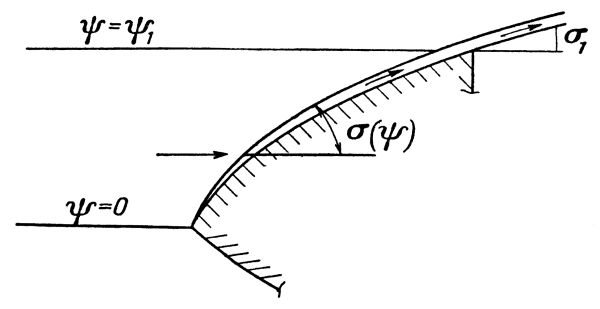 |
| Р и с. 20. Ударный слой в теории Ньютона. |
Введем для отношения сопротивления тела к величине U обозначение
![]()
![]() CD. Эта величина выражается так:
CD. Эта величина выражается так:
|
|
(3.2.8) |
Для плоских тел можно рассчитать часть подъемной силы, которая создается на одной стороне тела. Подъемная сила на единицу ширины тела определяется по формуле
|
|
(3.2.9) |
Приведенные выше формулы позволяют вычислить в квадратурах давление и силы для плоских и осесимметричных тел различной формы. Некоторые примеры таких расчетов будут даны в дальнейшем; много примеров можно найти в литературе, см., например, работы Айви, Кланкера и Боуэна [1], Айви и Мориссетте [1], которые развивали предложенную Буземаном [1] теорию.
Получим теперь некоторые результаты для структуры ударного слоя,
рассматривая модель ламинарного слоя. Массу, приходящуюся на единицу
площади поверхности ударного слоя
3),
обозначим через
![]() m.
Тогда будем иметь
m.
Тогда будем иметь
m = 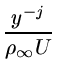 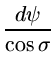 . .
|
(3.2.10) |
mоднород. = 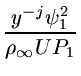 . .
|
(3.2.11) |
t = 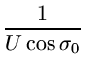 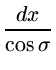
|
(3.2.12) |
Результаты ньютоновской теории обтекания для плоских и осесимметричных тел можно применить к значительно более широкому классу тел. Рассмотрим тело, состоящее из ряда поверхностей, в месте стыка которых имеются изломы. Потребуем, чтобы каждая отдельная поверхность была частью двумерной поверхности (поверхностью некоторого произвольного цилиндра с образующей, перпендикулярной направлению набегающего потока) или частью поверхности тела вращения с осью, параллельной направлению набегающего потока. Потребуем, чтобы все углы в месте пересечения поверхностей были выпуклыми и чтобы каждый из этих углов играл роль передней кромки для обоих указанных типов поверхностей.
Тогда на каждой поверхности мы можем рассматривать бесконечно тонкий ударный слой (или его меридиональное сечение для участков поверхностей вращения). В рамках ньютоновской теории обтекания течение в каждом из этих слоев не зависит от течения в соседнем слое, а давление и структура ударного слоя могут быть рассчитаны на основании теории плоского или осесимметричного течения, изложенной в этом разделе.
Возможно построить выпуклое тело и более общего вида. представляющее собой предельный случай этой составной поверхности; к такому телу также будет применима простая ньютоновская теория. Из-за сильного ограничения, заключающегося в том, что ни один из углов не может играть роль задней кромки для каждого участка поверхности, мы в этой концепции ограничены весьма специальным классом тел, который можно назвать «классом ньютоновских тел без поперечного течения».
Можно сделать дальнейшее обобщение, введя классическое понятие о цилиндрическом течении. В этом случае отдельные поверхности, из которых составляется тело, могут быть участками произвольных цилиндров, образующие которых не перпендикулярны направлению потока. Для таких поверхностей расчет давления и структуры слоя оказывается более трудным, а условие относительно ориентации изломов становится более сложным. Такие цилиндрические течения мы будем исследовать в § 3.6, но не будем при этом касаться их приложения к составным телам.
Задача определения такой формы тела, чтобы его сопротивление было минимальным, является старой задачей, которой Ньютон занимался еще в XVII веке. Однако результаты Ньютона, а также результаты Эггерса, Резникова и Денниса [1] основаны на решении, в котором не учитывается поправка к давлению на теле на центробежные силы. Мы же займемся здесь задачей об определении оптимальных форм, дающих минимальное сопротивление, используя при этом выражение для давления (3.2.7). Для сопротивления мы имеем формулу (3.2.8); надо заметить, что эта формула представляет собой нечто отличное по форме от той формулы, которая получается, если пользоваться неуточненным выражением для давления. Мы считаем удобным различать два типа оптимальных контуров, которые мы будем строить здесь и которые будем называть терминами «абсолютно оптимальный контур» и «относительно оптимальный контур».
Сначала мы будем интересоваться классической задачей, в которой заданными величинами являются длина и толщина тела. Используемый при этом метод будет или применен непосредственно, или приспособлен к задачам с иными изопериметрическими условиями. При рассмотрении тел вращения мы не будем заниматься телами с протоком; в случае необходимости такие тела можно рассмотреть с помощью тех же методов. Мы будем пользоваться такой постановкой задачи, в которой основной рассматриваемой функцией является y(x). Можно было бы применить также иные постановки, в которых рассматриваются функции x(y) или P(x). Однако применение в качестве основной функции y(x) представляется наиболее удобным.
Уравнение (3.2.8) для сопротивления является основным уравнением для решения задач об определении оптимальных контуров, и мы перепишем это уравнение еще раз:
|
|
(3.4.1) |
Сделаем теперь на первый взгляд наивное предположение о том, что два
множителя являются независимыми и что максимум произведения можно получить,
определяя отдельно максимумы сомножителей. Максимальное значение
cos![]() просто равно 1 и получается при
просто равно 1 и получается при
![]() = 0. Максимум P1 получаем методами
вариационного исчисления. При условии
cos
= 0. Максимум P1 получаем методами
вариационного исчисления. При условии
cos![]() = 1 требование о том, чтобы
толщина тела была задана, является несущественным, и наш аналитический
метод можно непосредственно применить и к такой задаче, в которой толщина
тела не является заданной. Однако тогда должна быть принята во внимание
вариация величины
= 1 требование о том, чтобы
толщина тела была задана, является несущественным, и наш аналитический
метод можно непосредственно применить и к такой задаче, в которой толщина
тела не является заданной. Однако тогда должна быть принята во внимание
вариация величины ![]() , стоящей в правой части уравнения (3.4.1).
, стоящей в правой части уравнения (3.4.1).
Этап решения, на котором мы положили
cos![]() = 1, является критическим и
должен быть в дальнейшем тщательно исследован. Если
cos
= 1, является критическим и
должен быть в дальнейшем тщательно исследован. Если
cos![]() = 1, то
сопротивление можно выразить с помощью формулы (3.2.4) в виде
= 1, то
сопротивление можно выразить с помощью формулы (3.2.4) в виде
|
|
(3.4.2) |
Для сравнения приведем соответствующее выражение для сопротивления, когда давление определяется по неуточненной формуле
|
|
(3.4.3) |
|
CD |
(3.4.4) |
Выразим P1 через y(x), учитывая, что
cos![]() = 1/
= 1/![]() .
Тогда
.
Тогда
P1 = 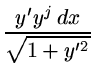 , ,
|
(3.4.5) |
|
(1 + j)V = |
(3.4.6) |
S = 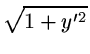 yj dx. yj dx.
|
(3.4.7) |
F = 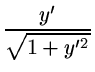 + + 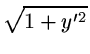 |
(3.4.8) |
|
F - y' |
(3.4.9) |
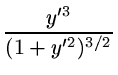 + + 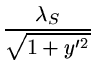 = Ay-j. = Ay-j.
|
(3.4.10) |
Простейшие решения уравнения (3.4.10) даны в табл. 1. Заметим, что при A = 0
(длина тела не задана) решения для плоского и для осесимметричного течения
одинаковы. Если в осесимметричном течении ![]() и
и ![]() равны нулю,
то решение можно представить в параметрическом виде
равны нулю,
то решение можно представить в параметрическом виде
x = 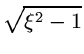 - - |
(3.4.11а) |
|
y = y0 |
(3.4.11б) |
y = y0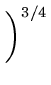 . .
|
(3.4.12) |
Решения, которые мы получили, соответствуют оптимальным телам только тогда,
когда можно считать, что
cos![]() = 1. Однако, вообще говоря, полученные
контуры имеют конечный наклон у кормового среза тела, и естественно
возникает вопрос, будет ли наше решение иметь смысл в этом случае. С
математической точки зрения не может быть возражений против наличия разрыва
в наклоне контура. Поэтому мы можем потребовать, чтобы наклон контура
непосредственно у заднего среза тела равнялся нулю, а на бесконечно малом
расстоянии от кормового среза оставался конечным. С физической точки зрения
для существования такого решения требуется, чтобы направление ударного слоя
внезапно изменялось, а это потребовало бы бесконечно большого
отрицательного давления, действующего на бесконечно малом участке тела
около кормового среза. Конечно, мы должны отказаться от принятия такого
механизма как нереального даже с точки зрения довольно нестрогих моделей
ньютоновской теории обтекания.
= 1. Однако, вообще говоря, полученные
контуры имеют конечный наклон у кормового среза тела, и естественно
возникает вопрос, будет ли наше решение иметь смысл в этом случае. С
математической точки зрения не может быть возражений против наличия разрыва
в наклоне контура. Поэтому мы можем потребовать, чтобы наклон контура
непосредственно у заднего среза тела равнялся нулю, а на бесконечно малом
расстоянии от кормового среза оставался конечным. С физической точки зрения
для существования такого решения требуется, чтобы направление ударного слоя
внезапно изменялось, а это потребовало бы бесконечно большого
отрицательного давления, действующего на бесконечно малом участке тела
около кормового среза. Конечно, мы должны отказаться от принятия такого
механизма как нереального даже с точки зрения довольно нестрогих моделей
ньютоновской теории обтекания.
Хейз У.Д., Пробстин Р.Ф. Теория гиперзвуковых течений. Ингиз, М., 1962.
Этот фрагмент книги в виде, подготовленном для печати в виде мини-брошюрки:
![]() probstin_ps.zip (134 K)
probstin_ps.zip (134 K)
|
Вариационное исчисление | Домашняя страница |