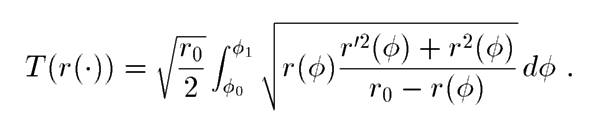
Семинар Отдела Динамических Систем
11 декабря 1996
А.Г.Иванов
Получен функционал времени спуска в задаче о брахистохроне в центральном поле тяготения:
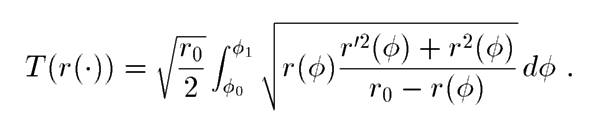
Здесь 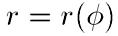 -- положение точки в полярной системе координат с
центром, совпадающим с центром тяготения.
-- положение точки в полярной системе координат с
центром, совпадающим с центром тяготения.
При нахождении минимума функционала используется метод Эйлера [1] -- приближение искомой кривой кусочно-линейной ломаной. Таким образом, задача сводится к нахождению минимума функции многих переменных. Минимизация проводится с помощью измененного метода Хука-Дживса. Этот метод отличается от стандартного метода Хука-Дживса [2] большей степенью перебора.
В рассматриваемой постановке задачи о брахистохроне определенный интерес представляет следующее исследование -- как изменяется время спуска по оптимальной траектории при изменении точки окончания процесса ("нижней" граничной точки), при этом начальная ("верхняя") точка фиксируется. Достаточной наглядностью обладают изохроны -- линии уровня времени оптимального спуска.
Для нахождения изохрон используется параллельная программа построения линий уровня, первоначальный вариант которой описан в [3]. Рассматриваются несколько вариантов алгоритма задачи-мастера. Проводится анализ эффективности распараллеливания для разных алгоритмов и различного числа процессоров.
Литература
[1] Л.Э.Эльсгольц. Вариационное исчисление. М.: Техгиз, 1958.
[2] Б.Банди. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.
[3] А.Г.Иванов. Опыт построения линий уровня на транспьютерных системах. // Алгоритмы и программные средства параллельных вычислений: [Сб. науч.тр.]. Екатеринбург: УрО РАН, 1995.
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru